Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.8 - Ex. 8

Em cada um dos problemas de 7 a 10:

(a) Encontre a solução do problema de valor inicial dado.

(b) Desenhe a trajetória da solução no plano x1x2 e desenhe, também, o gráfico de x1 em função de t.

x ' = - 5 2 3 2 - 3 2 1 2 x ,           x 0 = 3 - 1

Passo 1

a)Para determinarmos a solução geral do sistema temos que encontrar os autovalores e autovetores associados.

Para isto utilizaremos a seguinte relação:

A - r I ξ = 0

Em que os autovalores serão as raízes do d e t ⁡ ( A - r I ) .

Determinando os autovalores:

det ⁡ A - r I = - 5 2 3 2 - 3 2 1 2 - r 0 0 r

det ⁡ A - r I = - 5 2 - r 3 2 - 3 2 1 2 - r

det ⁡ A - r I = r 2 + 2 r + 1

Tendo as raízes:

r 1 = - 1

r 2 = - 1

Vamos agora determinar o autovetor associado, colocando r = - 1 , temos:

A - r I ξ = 0

- 5 2 + 1 3 2 - 3 2 1 2 + 1 ∙ ξ 1 ξ 2 = 0

Reduzindo o sistema para:

- ξ 1 + ξ 2 = 0

Para r = - 1 :

ξ 1 = 1 1

x ( 1 ) t = 1 1 ∙ e - t

Para podermos calcular a segunda solução linear, teremos que generalizar um verto próprio:

- 3 / 2   3 / 2 - 3 / 2 3 / 2 ∙ η 1 η 2 = 1 1

Temos que:

- 3 η 1 + 3 η 2 = 2

Assumindo η 1 = k , teremos:

η 2 = k + 2 3

Aplicando a segunda solução para autovalores repetidos:

x 2 = 1 1 t e - t + k 2 3 + k e - t = 1 1 t e - t + 0 2 / 3   e - t + k 1 1 e - t

Aplicando a formula da solução geral temos:

x = c 1 x 1 t + c 2 x ( 2 ) t

Logo a solução geral fica:

x = c 1 1 1 e - t + c 2 1 1 t e - t + 0 2 / 3   e - t

Aplicando as condições iniciais temos:

x 0 = 3 - 1

Ficamos com o seguinte sistema:

c 1 = 3

c 1 + 2 c 2 3 = - 1

Tendo resultado como:

c 1 = 3

c 2 = - 6

Portanto a solução específica é:

x = 3 - 1 e - t - 6 6 t e - t

Passo 2

b) desenhando os gráficos temos:

x 2   m e   f u n ç ã o   d e   x 1  

x 1   e m   f u n ç ã o   d e   ( t )

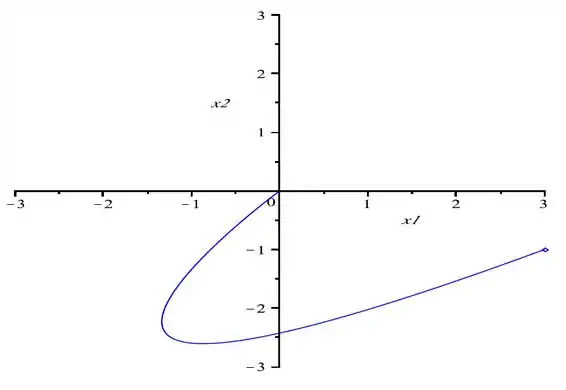
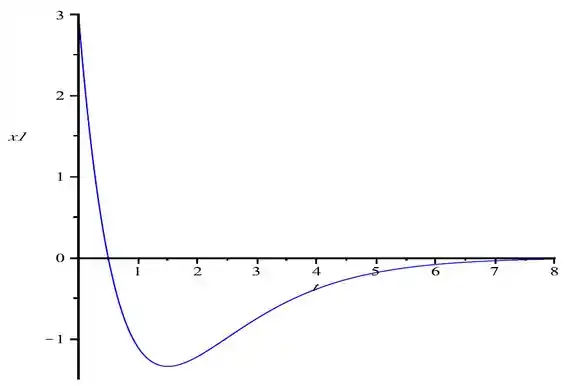
Resposta

a) x = 3 - 1 e - t - 6 6 t e - t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 9 a 14 , encontre a solução geral do sistema de equações dado. x ' = 1 1 1 2 1 - 1 - 8 - 5 - 3 x
Em cada um dos problemas de 1 a 6 : ( a ) Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando t → ∞ ( b ) Desenhe um campo de direções e faça o gráfico
Em cada um dos problemas de 1 a 6 : ( a ) Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando t → ∞ ( b ) Desenhe um campo de direções e faça o gráfico
Em cada um dos Problemas 7 e 8 : ( a ) Encontre a solução geral do sistema de equações dado ( b ) Desenhe um campo de direções e algumas das trajetórias. Em cada um desses, a matriz de coeficientes te
Em cada um dos problemas de 1 a 6 : ( a ) Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando t → ∞ ( b ) Desenhe um campo de direções e faça o gráfico