Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 5.2 - Ex. 18
Em cada um dos problemas de 15 a 18:
- Encontre os cinco primeiros termos não nulos na solução do problema de valor inicial dado.
- Faça gráficos das aproximações da solução com quatro e cinco termos no mesmo conjunto de eixos.
- Estime, a partir dos gráficos no item (b), o intervalo no qual a aproximação com quatro termos é razoavelmente precisa.
Passo 1
Nesse problema iremos utilizar a forma de série de potências para encontrarmos a solução da nossa EDO. Vamos primeiro supor que a solução seja algo do tipo:
Usando as informações dadas no enunciado, vamos derivar duas vezes essa expressão para encontrarmos e e depois de encontrarmos a solução, vamos aplicar as condições iniciais para obtermos os quatro primeiros termos não nulos da solução.
Passo 2
- Bom, como sugerido pelo próprio enunciado, vamos usar o resultado do problema 12 para facilitar nossas vidas rsrs. Temos que o problema 12 nos dá
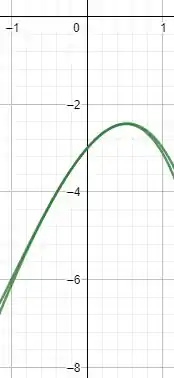
- Plotando essas duas curvas nos dá o seguinte gráfico.
- Observando o gráfico, conseguimos ver que entre a aproximação com apenas quatro termos é um tanto quanto precisa por coincidir bem com a de cinco termos.
Nossa solução geral é então e . Se colocarmos e , teremos que
e temos também que , assim vamos ter que:
Expandindo nossa equação nos dá
Nos dando que o quarto e quinto termo do polinômio é aproximadamente
Passo 3
Passo 4
Resposta
c)
Exercícios de Livros Relacionados
Use série de potência para resolver a equação diferencial. y ' ' = y
Use série de potência para resolver a equação diferencial. y ' ' + x y ' + y = 0
Use série de potência para resolver a equação diferencial. ( x - 1 ) y ' ' + y ' = 0
Use série de potência para resolver a equação diferencial. y ' ' + x 2 y ' + x y = 0 ,y 0 = 0 ,y ' 0 = 1
Use série de potência para resolver a equação diferencial. y ' ' - x y ' - y = 0 ,y 0 = 1 ,y ' 0 = 0