Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.1 - Ex. 23
Em cada um dos problemas de 21 a 23:
- Desenheum campo de direções para a equação diferencial dada. Como parece que as soluções se comportam quando assume valores grandes? O comportamento depende da escolha do valor inicial ? Seja o valor de no qual ocorre a transição de um tipode comportamento para outro. Estime o valor de .
- Resolva o problema de valor inicial e encontre precisamente o valor crítico .
- Descreva o comportamento da solução correspondente ao valor inicial .
Passo 1
Para resolvermos esse problema vamos fazer o campo de direção com a ajuda de um software, que no meu caso será o GeoGebra, e depois iremos analisar o tipo de EDO que temos para resolver o problema de valor inicial usando fator integrante, onde
e a solução sendo dada por
Vamos resolver!!
Passo 2
- Bom, primeiro vamos fazer nosso campo de direções. Temos que ele será algo mais ou menos dessa forma
- Pela equação dada no passo 1, temos que para encontrar nosso fator integrante, temos que primeiramente encontrar . Pela forma da equação diferencial, temos que nosso será . Assim, nosso fator integrante fica
- Bom, temos que no nosso valor de , como deveria ser, toda a expressão para será zero. Assim, nossa equação fica
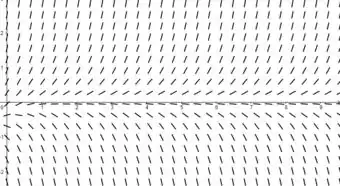
Vemos que para um , o campo de direções tende a crescer infinitamente em uma grande escala de valores que dependerão de . Outra coisa que podemos notar é que o campo tende a ficar horizontal em um valor próximo a .
Passo 3
E a nossa solução será
Usando integração por partes, vamos chegar que
Se aplicarmos a condição de contorno, onde , teremos que
Substituindo na equação original, vemos que
Como é um ponto de crítico, temos que a natureza das soluções só irá mudar quando
Ou seja:
Passo 4
E para essa equação, vemos que para quanto maior for nosso , mais tende para zero.
Resposta
(b)
(c)