Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 32
Os Problemas e tratam do circuito elétrico pelo sistema de equações diferenciais dado no Problema da Seção :
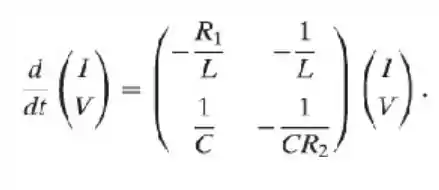
32- Encontre a solução geral da Eq. (i) se e
Mostre que e quando , independente dos valores iniciais e .
Passo 1
O melhor passo aqui é substituir os valores que nos foi dado e fazer:
Então:
Agora encontrando o auto valor teremos:
Cujas raízes (resultados dos autovalores) serão:
Passo 2
Agora para encontrar os autovetores, começando para :
Nessa teremos a relação entre igual a:
O que nos dá um auto vetor igual a:
Então a solução será:
Passo 3
Agora para teremos o autovetor :
Logo:
Então a relação nos dará o autovetor:
E a solução será:
Logo a solução geral da solução será:
Mas como então temos:
Passo 4
Como os expoentes são negativos (por conta dos autovalores) isso é e , então quando toda a solução tenderá a zero. Isso independentemente do valor de e de ,