Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 4

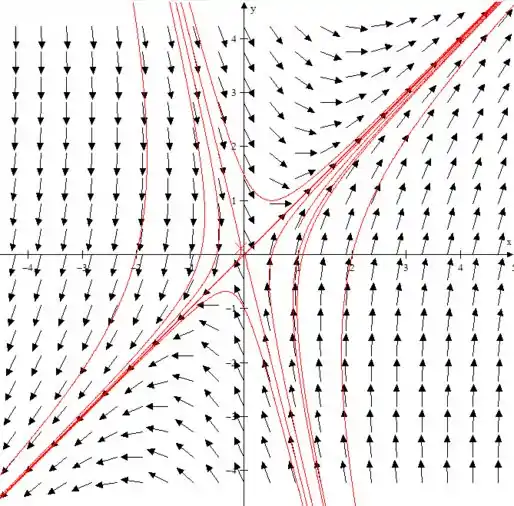
Em cada um dos problemas de 1 a 6 :

( a ) Encontre a solução geral do sistema de equações dado e descreva o comportamento das soluções quando t → ∞

( b ) Desenhe um campo de direções e faça o gráfico de algumas trajetórias do sistema

x ' = 1 1 4 - 2 x

Passo 1

Primeiramente vamos encontrar os autovalores dessa matriz ao fazer:

det ⁡ 1 - r 1 4 - 2 - r = 0

Fazendo essa determinante teremos:

1 - r - 2 - r - 4 = 0

r 2 + 2 - 1 r - 4 - 2 = 0 → r 2 + r - 6 = 0

Então os auto vetores serão:

r 1 ; r 2 = ( - 3 ; 2 )

Passo 2

Como vimos nesse capítulo e nas questões anteriores a solução geral desse sistema é dado por:

x = c 1 e r 1 t ξ 1 + c 2 e r 2 t ξ 2

Onde ξ 1 e ξ 2 são autovetores associados e a esses autovalores e ξ 1 1 e ξ 2 1 são variáveis internas que compõem o autovetor ξ 1 .

Encontrando o auto vetor associado ao autovalor r = - 3 teremos:

1 + 3 1 4 - 2 + 3 ξ 1 1 ξ 2 1 = 0

4 1 4 1 ξ 1 1 ξ 2 1 = 0

Onde encontraremos uma relação entre ξ 1 1 e ξ 2 1 iguais a:

4 ξ 1 1 = - ξ 2 1

Portanto a solução para isso é :

ξ 1 = ξ 1 1 ξ 2 1 = 1 - 4

Nos dando uma solução igual a:

x 1 = c 1 1 - 4 e - 3 t  

Passo 3

Agora o autovetor para r = 2 será:

1 - 2 1 4 - 2 - 2 ξ 1 2 ξ 2 2 = 0

- 1 1 4 - 4 ξ 1 2 ξ 2 2 = 0

Isso nos dará uma relação entre ξ s igual a:

ξ 1 2 = ξ 2 2

Logo o autovetor será:

ξ 2 = ξ 1 2 ξ 2 2 = 1 1

Nos dando uma solução igual a:

x 2 = c 2 1 1 e 2 t  

Logo a solução geral do sistema é:

x = c 1 1 - 4 e - 3 t + c 2 1 1 e 2 t  

Passo 4

Resposta

a ) x = c 1 1 - 4 e - 3 t + c 2 1 1 e 2 t  

b )   I m a g e m   d o   P a s s o   4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos Problemas 9 e 10 , encontre a solução do problema de valor inicial dado. Descreva o comportamento da solução quando t → ∞ x ' = 1 - 5 1 - 3 x , x 0 = 1 1
Em cada um dos problemas de 13 a 20, a matriz de coeficientes contém um parâmetro α. Em cada um desses problemas: (a) Determine os autovalores em função de α. (b) Encontre o valor ou valores críticos
Em cada um dos problemas de 1 a 6 : ( a ) Expresse a solução geral do sistema de equações dado como combinação e de funções reais ( b ) Desenhe, também um campo de direções, esboce algumas trajetórias
Em cada um dos problemas de 1 a 6 : ( a ) Expresse a solução geral do sistema de equações dado como combinação e de funções reais ( b ) Desenhe, também um campo de direções, esboce algumas trajetórias
Em cada um dos problemas de 1 a 6 : ( a ) Expresse a solução geral do sistema de equações dado como combinação e de funções reais ( b ) Desenhe, também um campo de direções, esboce algumas trajetórias