Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 2
Em cada um dos problemas de a :
Expresse a solução geral do sistema de equações dado como combinação e de funções reais
Desenhe, também um campo de direções, esboce algumas trajetórias e descreva o comportamento das soluções quando
Passo 1
Descobrindo o valor dos autovalores desse sistema nós teremos:
Fazendo a determinante temos:
Fazendo Bhaskara encontramos raízes iguais a:
E como temos raízes complexas com parte real igual então nossa solução fica da seguinte maneira:
Sem nenhum valor de constante.
Passo 2
Então o autovetor para será:
E que nos dará:
E conseguimos ver uma relação igual a:
Uma relação entre ambos será:
O que dá certo se substituirmos na linha de baixo.
De forma que a primeira solução será igual a:
Arrumando a casa nós teremos:
Se fizermos o outro autovalor ( ) nós encontraremos um autovetor igual a:
E uma outra solução igual a:
Portanto podemos pegar qualquer uma das soluções como soluções do nosso sistema no caso vamos pegar a primeira e que será:
Passo 3
Agora plotando o campo de direções nós iremos ter:
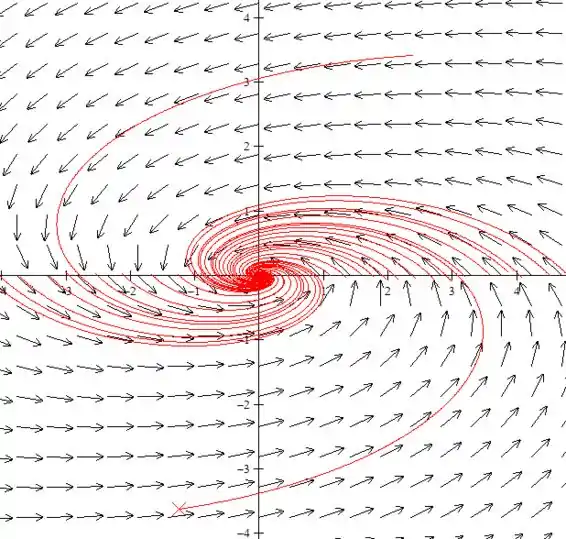
Já este conseguimos dizer que quando a solução tende a zero, pois todos os valores iniciais tendem a origem.
Isso é muito por conta do termo