Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.1 - Ex. 3
Em cada um dos problemas de a , esboce o gráfico da função dada. Em cada caso, determine se é continua, seccionalmente contínua, ou nenhuma das duas no intervalo .
3.
Passo 1
O gráfico da função dada fica o seguinte:
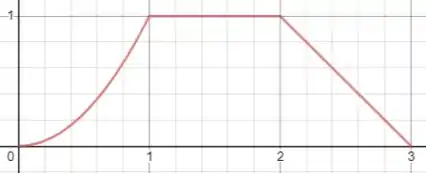
Como podemos ver, o gráfico só tem pontos de singularidade em e , mas a função ainda é contínua no intervalo que a questão deu.
Resposta
Exercícios de Livros Relacionados
Lembre que c o s b t = e i b t + e - i b t 2 e que s e n b t = e i b t - e - i b t 2 i . Em cada um dos problemas de 11 a 14, encontre a transformada de Laplace da função dada; a e b são constantes re
Lembre que c o s b t = e i b t + e - i b t 2 e que s e n b t = e i b t - e - i b t 2 i . Em cada um dos problemas de 11 a 14, encontre a transformada de Laplace da função dada; a e b são constantes re
Em cada um dos problemas de 15 a 20, use integração por partes para encontrar a transformada de Laplace da função dada; n é um inteiro positivo e a é uma constante real.19. f t = t 2 sin a t
Encontre a transformada de Laplace de cada uma das funções a seguir: a )f( t )=t b )f( t )=t 2 c )f t = t n Em que n é um número inteiro positivo.
Considere a transformada de Laplace de t p em que p- 1 .A - Usando o problema 30, mostre que L t p = ∫ 0 ∞ e - s t t pd t = 1 s p + 1 ∫ 0 ∞ e - x x p d x = = Γ p + 1 / s p + 1 ,s0 B - Seja p um inteir