Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.8 - Ex. 9
Em cada um dos problemas de 9 e 10, seja e use o método das aproximações sucessivas para resolver o problema de valor inicial dado.
- Calcule
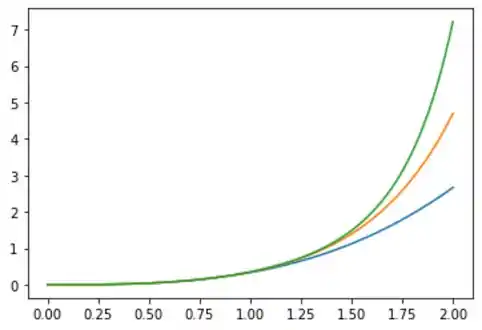
- Faça o gráfico de e observe se os iterados parecem estar convergindo.
Passo 1
Se supusermos, temporatiamente, que existe uma função que satifaz o problema de valor inicial, então é uma função contínui que só depende de . Logo, podemos integrar do ponto inicial até um valor arbitrário de , obtendo
Em que usamos a condição inicial . Usamos também para denotar a variável de integração.
Passo 2
(a) Assim vamos usar a suposição dada no passo 1 e prevista no Teorema 2.8.1 e vamos fazer que
Assim tomando que
Seguindo temos
Passo 3
(b) Plotando o nosso pequeno graficozinho, onde temos que
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos problemas 9-16, determine, por inspeção, pelo menos uma solução para a equação diferencial dada. d y d x = 5 y
Nos problemas 5-8, verifique que a função indicada é uma solução para a equação diferencial dada. x 2 y ' ' + x y ' + y = 0 ; y = c 1 . cos ( l n ( x ) ) + c 2 . s e n ln x ,x0
Nos problemas 1-10, determine uma região do plano x y para a qual a equação diferencial teria uma única solução passando por um ponto ( x 0 , y 0 ) na região. d y d x = y 2 3
Explique por que y = tan x não é uma solução para o problema de valor inicial d y d x = 1 + y 2 , y 0 = 0 No intervalo ( - 2,2 )
Por inspeção, encontre uma solução para o problema de valor inicial y ' = y - 1 , y 0 = 1 Diga por que as condições do Teorema 2.1 não são satisfeitas para essa equação diferencial. Embora não possamo