Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 1i
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Passo 1
Esse item nos fornece o seguinte par de equações paramétricas:
Vamos começar substituindo o parâmetro das equações paramétricas por alguns valores do intervalo :
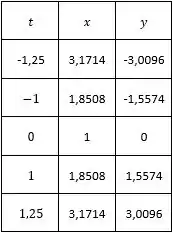
Passo 2
Esboçando a curva descrita pelas equações paramétricas a partir dos pontos presentes na tabela chegaremos em algo parecido com isso:
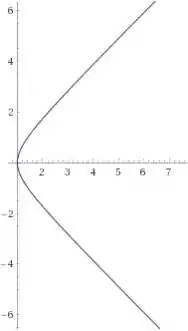
Passo 3
Para determinarmos a equação cartesiana dessa curva a partir do par de equações paramétricas devemos eliminar o parâmetro , para isso devemos nos lembrar da seguinte identidade trigonométrica:
Tendo isso como base, basta realizarmos as seguintes manipulações na equação :
Onde nessa forma é possível identificar uma possível substituição já que :
Resposta
Ei, a resposta está no passo a passo :)