Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.8 - Ex. 21

Calcular int_0^4 int_0^((1)/(4) sqrt(144 - 9 y^2)) ( 144 - 16 x^2 - 9 y^2 ) d x d y .

Passo 1

A representação gráfica se dá:

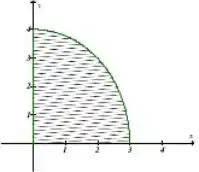
Passo 2

Para facilitar a resolução da questão, utilizaremos a seguinte transformação:

x = 3 u e y = 4 v

O jacobiano dessa transformação será igual a 6:

J = |[[3,0],[0,4]]| = 12

A nova figura se dará como um círculo de raio 1 centrado na origem.

Então, substituindo na equação dada, temos:

∬ ( 144 - 16 * 9 u^2 - 9 * 16 v^2 ) * 12 d u d v = 1728 ∬ ( 1 - u^2 - v^2 ) d u d v

Nesse caso, as coordenadas polares se dão:

u = r cos theta ; v = r s e n theta ; u^2 + v^2 = r^2

Substituindo novamente. Obtemos:

1728 ∬ ( 1 - r^2 ) * r d r d theta = 1728 ∬ ( r - r^3 ) * r d r d theta

Com

0 <= r <= 1

0 <= theta <= (pi)/(2)

Passo 3

Integrando para r :

1728 int_0^1 ( r - r^3 ) d r = 1728 ((r^2)/(2) - (r^4)/(4))

Aplicando os limites:

1728 [(1 - 0) (1)/(2) - (1 - 0) (1)/(4)] = 432

Passo 4

Integrando para theta :

int_0^((pi)/(2)) 432 d theta = 432 theta

Aplicando os limites:

((pi)/(2) - 0) * 432 = 216 pi

Resposta

216 pi

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região cuja área é dada pela integral e calcule-a ∫ π / 2 π∫ 0 2 sen ⁡ θ r d r d θ
A região limitada por ambos cardioides r = 1 + cos theta e r = 1 - cos theta
Calcule a integral dada, colocando-a em coordenadas polares. ∬ R y 2 x 2 + y 2 d A Onde R é a região que fica entre os círculos x 2 + y 2 = a 2 e x 2 + y 2 = b 2 com 0ab .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ R 2 x - y d A Onde R é a região do primeiro quadrante limitada pelo círculo x 2 + y 2 = 4 e as retas x = 0 e y = x .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ D cos ⁡ x 2 + y 2 d A Onde D é o disco com centro na origem e raio 2.