Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 10

Calcule a integral dada, colocando-a em coordenadas polares.

10.

∬ R y 2 x 2 + y 2 d A

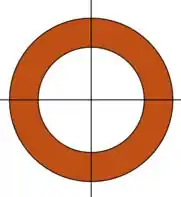
Onde R é a região que fica entre os círculos x 2 + y 2 = a 2 e x 2 + y 2 = b 2 com 0 < a < b .

Passo 1

Fala, galeraaa!

Essa questão pede pra gente transformar nossa função, que está em coordenadas cartesianas, em coordenadas polares! Moleza!

Relembrando algumas fórmulas polares:

y = r s e n θ x = r c o s θ x 2 + y 2 = r 2 d A = r   d r   d θ

Substituindo as informações que temos, vamos analisar nossa função:

∬ R y 2 x 2 + y 2 d A

Onde

y 2 = r 2 sen 2 ⁡ θ  

  x 2 + y 2 = r 2

Logo, realizando também as substituições e teremos:

∬ R y 2 x 2 + y 2 d A

∬ R r 2 sen 2 ⁡ θ r 2 r d r d θ

∬ R sen 2 ⁡ θ r d r d θ

Agora, vamos achar nossos limites de integração.

O valor do raio r varia de a até b (região entre os círculos), e o valor de θ varia de 0 até 2 π , pois a nossa região R descreve todo o anel circular de raio externo b e raio interno a .

Passo 2

Agora que descrevemos a região em coordenadas polares, podemos colocar os limites de integração na nossa integral. Portanto,

∫ 0 2 π ∫ a b sen 2 ⁡ θ r d r d θ

Vamos resolver primeiro a integral interna:

∫ a b sen 2 ⁡ θ r d r

sen 2 ⁡ θ ∫ a b r d r

sen 2 ⁡ θ ⋅ r 2 2 a b

= s e n 2 θ ⋅ b 2 2 - a 2 2

Passo 3

Vamos resolver a integral de fora:

∫ 0 2 π b 2 - a 2 2 ⋅ sen 2 ⁡ θ d θ

Sabendo que

s e n 2 θ = 1 - cos ⁡ 2 θ 2 ⁡  

Então,

∫ 0 2 π b 2 - a 2 2 ⋅ 1 - cos ⁡ 2 θ 2 d θ

Jogamos o que não tem θ pra fora da integral, porque “imaginamos” que seja uma constante:

b 2 - a 2 2 ⋅ ∫ 0 2 π 1 - cos ⁡ 2 θ 2 d θ

b 2 - a 2 2 ⋅ θ - sen ⁡ 2 θ 2 2 0 2 π = b 2 - a 2 2 ⋅ π

Resposta

∬ R y 2 x 2 + y 2 d A = b 2 - a 2 2 ⋅ π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pulverizador agrícola distribui água em um padrão circular de 50m de raio. Ele fornece água até uma profundidade de e - r metros por hora a uma distância de r metros do pulverizador.(a) Se 0R ≤ 100
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste para oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade nor
Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , yd A como uma integral iterada, onde f é uma função qualquer contínua em R .
Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , yd A como uma integral iterada, onde f é uma função qualquer contínua em R .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ R 4 - x 2 - y 2d A , onde R = x , yx 2 + y 2 ≤ 4 ,x ≥ 0 } .