Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 94b
Encontrar todos os pontos onde o gráfico de tem tangente horizontal. Usando uma ferramenta gráfica, esboçar o gráfico de e e comparar os resultados.
b)
Passo 1
A função tem reta tangente horizontal nos pontos onde a derivada é zero. Vamos começar derivando a função então...
Igualando a zero...
Isso ocorre quando...
Esses são todos os pontos onde a tangente é horizontal.
Passo 2
Vamos ver isso graficamente agora, no Geogebra:
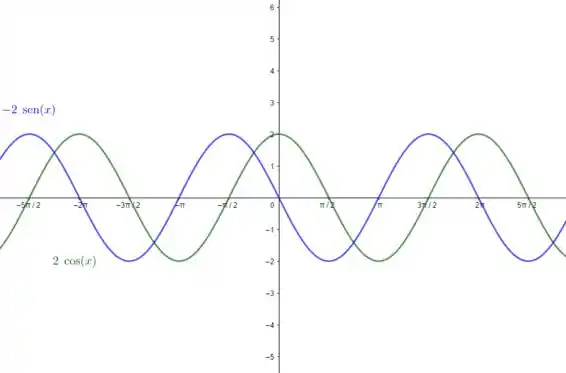
Aí está os resultados que encontramos😉
Resposta
Exercícios de Livros Relacionados
Encontrar todos os pontos onde o gráfico de f ( x ) tem tangente horizontal . Usando uma ferramenta gráfica, esboçar o gráfico de f ( x ) e f ' ( x ) e comparar os resultados. f x = s e n2 x
Calcular a derivada. f x = 3t g 2 x + 1 + x
Encontre f ' ( x ) : f x = 2 s e n 2 ( x )
Encontre f ' ( x ) : f x = 5 - cos x 5 + s e n ( x )
Encontre f ' ( x ) : f x = 4 cos x + 2 sen ( x )