Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.10 - Ex. 23

Calcular a área região delimitada pela curva

x^((2)/(3)) + y^((2)/(3)) = 1

Passo 1

A área se dá pelo seguinte gráfico:

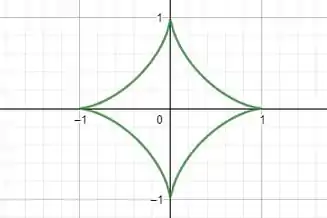
Passo 2

A equação da área se dá:

A = ∬ d A

Vamos utilizar de transformações para facilitar a resolução:

x^((1)/(3)) = u e y^((1)/(3)) = v

J = |[[3,u^2,0],[0,3,v^2]]| = 9 u^2 v^2

Assim, a equação da área fica:

A = ∬ d A = ∬ 9 u^2 v^2 d u d v

Passo 3

Agora, passaremos para coordenadas polares:

A = ∬ 9 u^2 v^2 d u d v = ∬ (9 r^4 cos^2 theta s e n^2 theta) * r d r d theta = ∬ (9 r^5 cos^2 theta s e n^2 theta) d r d theta

Ao realizarmos essas transformações, temos uma circunferência centrada na origem de raio igual a 1, então:

0 <= r <= 1

0 <= theta <= 2 pi

Assim:

A = int_0^(2 pi) int_0^1 9 r^5 cos^2 theta s e n^2 theta d r d theta

Passo 4

Integrando para r :

int_0^1 9 r^5 cos^2 theta s e n^2 theta d r = (9)/(6) r^6 cos^2 theta s e n^2 theta

Aplicando os limites:

(1 - 0) * (9)/(6) cos^2 theta s e n^2 theta = (3)/(2) cos^2 theta s e n^2 theta

Passo 5

Integrando para theta :

int_0^(2 pi) (3)/(2) cos^2 theta s e n^2 theta d theta = (3)/(16) theta - (3)/(64) s e n 4 theta

Aplicando os limites:

(2 pi - 0) * (3)/(16) - (s e n 8 pi - s e n 0) * (3)/(64) = (3 pi)/(8)

Resposta

(3 pi)/(8) u . a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule
Calcule
Calcule
Calcule
Calcule