Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 7.4 - Ex. 41

Calcular a área sob o gráfico de y = cos^6 x , de 0 até pi .

Passo 1

Para encontrar a região da área vamos primeiro desenhar a curva y = cos^6 x :

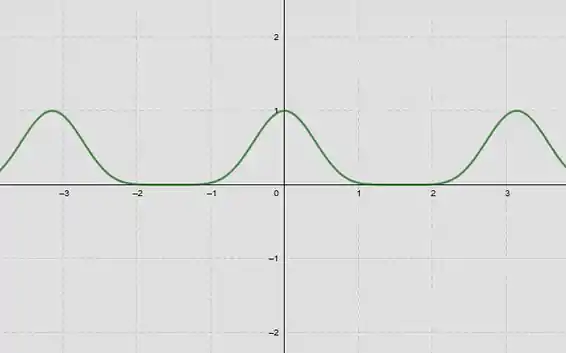
Passo 2

Pronto, temos o desenho base do gráfico. Agora vamos colocar as retas, elas vão limitar a área que queremos:

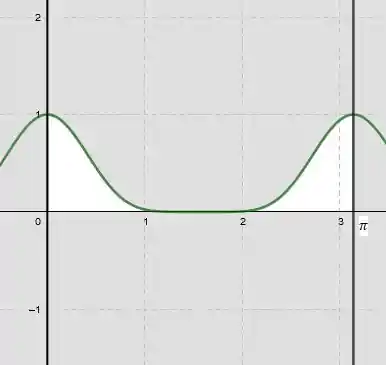
Passo 3

Vamos agora montar a integral da área, temos que os limites de integração são de 0 até pi , e temos que y = cos^6 x é a função de cima, e y = 0 é a função de baixo, vamos substituir:

A = int_a^b (f_c i m a - f_b a i x o) d x = int_0^(pi) (cos^6 x - 0) d x = int_0^(pi) cos^6 x d x

Para calcular int_0^(pi) cos^6 x d x vamos usar a fórmula de Recorrência, e vamos calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:

int cos^n u d u = (1)/(n) cos^(n - 1) u sen u + (n - 1)/(n) int cos^(n - 2) u d u

Assim:

int cos^6 x d u = (1)/(6) cos^(6 - 1) x sen x + (6 - 1)/(6) int cos^(6 - 2) x d x =

= (1)/(6) cos^5 x sen x + (5)/(6) int cos^4 x d x

Passo 4

Vamos usar a fórmula de Recorrência novamente para calcular essa integral que achamos:

int cos^4 x d x = (1)/(4) cos^(4 - 1) x sen x + (4 - 1)/(4) int cos^(4 - 2) x d x =

= (1)/(4) cos^3 x sen x + (3)/(4) int cos^2 x d x

Vamos usar a identidade para calcular a segunda integral que achamos:

cos^2 x = (1)/(2) + (cos (2 x))/(2)

int cos^2 x d x = int (1)/(2) + (cos (2 x))/(2) d x = int (1)/(2) d x + int (cos (2 x))/(2) d x = (1)/(2) x + (sen (2 x))/(4) + C

Agora é só juntar tudo:

int cos^6 x d x = (1)/(6) cos^5 x sen x + (5)/(6) int cos^4 x d x =

= (1)/(6) cos^5 x sen x + (5)/(6) ((1)/(4) cos^3 x sen x + (3)/(4) int cos^2 x d x) =

= (1)/(6) cos^5 x sen x + (5)/(6) ((1)/(4) cos^3 x sen x + (3)/(4) ((1)/(2) x + (sen (2 x))/(4))) + C

Passo 5

Pronto, já encontramos a integral indefinida, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:

int_a^b f (x) d x = F (b) - F (a)

Agora é só juntar tudo para achar a área:

A int_0^(pi) cos^6 x d x = ((1)/(6) cos^5 x sen x + (5)/(6) ((1)/(4) cos^3 x sen x + (3)/(4) ((1)/(2) x + (sen (2 x))/(4))))_0^(pi) =

= (1)/(6) cos^5 pi sen pi + (5)/(6) ((1)/(4) cos^3 pi sen pi + (3)/(4) ((1)/(2) pi + (sen (2 pi))/(4))) - ((1)/(6) cos^5 0 sen 0 + (5)/(6) ((1)/(4) cos^3 0 sen 0 + (3)/(4) ((1)/(2) * 0 + (sen (2 * 0))/(4)))) =

= (1)/(6) * (- 1)^5 * 0 + (5)/(6) ((1)/(4) * (- 1) * 0 + (3)/(4) ((1)/(2) pi + (0)/(4))) - ((1)/(6) * 1 * 0 + (5)/(6) ((1)/(4) * 1 * 0 + (3)/(4) ((1)/(2) * 0 + (0)/(4)))) = (5)/(6) ((3 pi)/(8)) = (5 pi)/(16)

Resposta

A = (5 pi)/(16)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integralint cot^3 (alpha) csc^3 (alpha) d alpha
Calcule a integralint tan^5 (x) d x
Calcule a integralint sec^6 (t) d t
Calcule a integralint ((tan^3 (theta))/(cos^4 (theta))) d theta
Calcule a integralint x tan (x) s e c (x) d x