Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 50
Calcular a derivada. A seguir, usando um software algébrico, comparar os resultados.
Passo 1
Vamos lá, aqui é exponencial. Vai ficar assim:
Prontinho! É isso😊
Passo 2
Vamos dar uma conferida básica (porque a questão pede) no CAS do Geogebra:
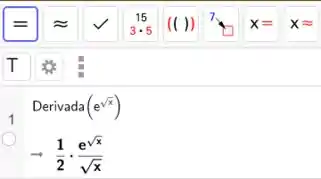
Tá certinho😊
Resposta
Exercícios de Livros Relacionados
Use o método do Exemplo 3 para ajudar a efetuar a derivação indicada: d d x [ ln x - 1 3 ( x 2 + 1 ) 4 ]
Encontre d y d x : y = l o g ( s e n 2 x )
Encontre d y d x : y = ln tg x
Encontre d y d x : y = s e n 2 ( ln x )
Encontre d y d x : y = l n ( ln ln x )