Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 51

Calcular a derivada. A seguir, usando um software algébrico, comparar os resultados.

f x = 1 2 - ln ⁡ 2 x

Passo 1

Aqui primeiro a gente tem que aplicar uma regrinha que é assim:

a b = e b l n   a

Trazendo pro nosso caso fica assim:

1 2 - ln ⁡ 2 x = e - ln ⁡ 2 x ln ⁡ 1 2  

Agora a gente deriva:

e - ln 2 x ( ln ⁡ 1 2 )   ⁡ - 1 2 x ( 2 ) ln ⁡ 1 2

(aqui a gente derivou o expoente)

e - ln ⁡ 2 x ln ⁡ 1 2 - ln ⁡ 1 2 x

Prontinho! Essa aí é a derivada😉

Passo 2

Vamos dar uma conferida básica (porque a questão pede) no site Solumaths. O site dá essa resposta aqui:

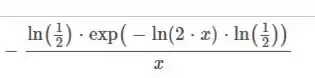
Tá certinho😊

Resposta

e - ln ⁡ 2 x ln ⁡ 1 2 - ln ⁡ 1 2 x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma funçãof tal que y = f( x ) satisfaz d y / d x=e - y , com y=0 quando x=0 .
Encontre:y = l o g_x e
Encontre a equação da reta tangente ao gráfico de y = f ( x ) em x = x 0 , se: f x = l o g ⁡ ( x ) x 0 = 10
Encontre:y = l o g_(1)/(x) e
Encontre:y = l o g_l n ( x ) e