Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 62
Calcular a derivada. A seguir, usando um software algébrico, comparar os resultados.
Passo 1
A gente sabe que né? Aí a derivada daria zero. Mas vamos calcular do jeito tradicional pra praticar...
Prontinho, deu zero como esperávamos😉
Passo 2
Vamos dar uma conferida básica (porque a questão pede) no site WorframAlpha. O site dá essa resposta aqui:
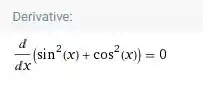
Certinho galera (só que no nosso caso é 😉
Resposta
Exercícios de Livros Relacionados
39-50 Encontre os limites.49. lim x → π / 4 1 - tg x sen x - cos x
39-50 Encontre os limites.47. lim θ → 0 cos θ - 1 2 θ 2
1 – 16 Derive.1. f x = x 2 sen x
1 – 16 Derive.15. f t = t e t co tg t
1 – 16 Derive.14. y = sen t 1 + tg t