Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.16 - Ex. 61
Calcular a derivada. A seguir, usando um software algébrico, comparar os resultados.
Passo 1
A gente pode reescrever pra facilitar nossa vida. Assim ó:
Beleza, agora ficou molezinha. Só derivar...
Prontinho! Essa é a derivada😉
Passo 2
Vamos dar uma conferida básica (porque a questão pede) no site WorframAlpha. O site dá essa resposta aqui:
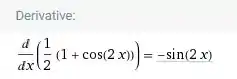
Certinho galera (só que no nosso caso é 😉
Resposta
Exercícios de Livros Relacionados
1 – 16 Derive.3. f x = e x cos x
Derive. y = e u( c o su+c u )
21-24 Encontre a equação da reta tangente à curva no ponto dado:21. y = se n x + co s x ,0,1
Derive:4) y = 2 . s e cx - co ssec x
Derive. h ( θ ) = c o s s e cθ+e θc o t gθ