Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.9 - Ex. 33

Utilize coordenadas esféricas.

a) Determine o centroide do hemisfério sólido homogêneo de raio a .

b) Determine o momento de inércia do sólido da parte (a) em relação a um diâmetro de sua base.

Passo 1

A questão pede para encontramos o centro de massa e o momento de inércia de um hemisfério de raio a com distribuição uniforme de massa. Desta forma, podemos calcular sua densidade δ (que é constante) fazendo

δ = m V = m 1 2 ⋅ 4 3 π a 3 = 3 m 2 π a 3

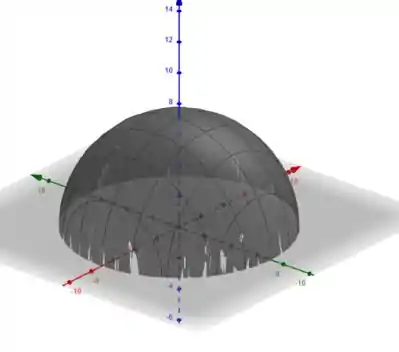
Nessa quest��o, precisamos identificar a equação da figura, assim como seus limites de integração, e após isso aplicar as equações do centro de massa e momento de inércia.

Perceba que a figura é idêntica em relação aos eixos x e y . O que significa que os centro de massas estarão posicionados sobre esses eixos. De modo que temos que encontrar apenas em z .

Passo 2

Além disso, vamos posicionar o hemisfério com eixo de simetria no eixo z : x 2 + y 2 + z 2 = a 2 , com z ≥ 0 . Assim, o domínio de integração será, em coordenadas esféricas:

D = ρ , θ , ϕ     0 ≤ ρ ≤ a ,   0 ≤ θ ≤ 2 π ,   0 ≤ ϕ ≤ π / 2 }

Devido a simetria do problema, vemos que x - = y - = 0 . Só precisamos achar z - :

z - = 1 m ∭ D z   δ   d V = 3 2 π a 3 ∫ 0 2 π ∫ 0 π / 2 ∫ 0 a ρ cos ⁡ ϕ ⋅ ρ 2   s e n ϕ   d ρ   d ϕ   d θ

Ou ainda,

z - = 3 a 3   ∫ 0 a ρ 3   d ρ ��� 0 π 2 s e n   2 ϕ 2   d ϕ

Usei que s e n   2 x = 2   s e n   x cos ⁡ x .

Para o momento de inércia, temos que

I = ∭ D d 2   δ   d V ,

onde d é a distância até o eixo com relação ao qual calculamos o momento de inércia. Como neste caso vamos calcular o momento de inércia com relação a um diâmetro da base, podemos toma-lo como sendo o eixo y . A distância de um ponto genérico ( x , y , z ) ao eixo y :

d 2 = x 2 + z 2

Em coordenadas esféricas, teremos

d 2 = ρ 2 s e n 2 ϕ cos 2 ⁡ θ + ρ 2 cos 2 ⁡ ϕ

Assim,

I = δ ∫ 0 2 π ∫ 0 π / 2 ∫ 0 a ρ 2 s e n 2 ϕ cos 2 ⁡ θ + ρ 2 cos 2 ⁡ ϕ ρ 2   s e n   ϕ   d ρ   d ϕ   d θ

Portanto,

I = δ ∫ 0 a ρ 4   d ρ ∫ 0 π / 2 ∫ 0 2 π s e n 3 ϕ cos 2 ⁡ θ + cos 2 ⁡ ϕ   s e n   ϕ   d θ   d ϕ

Passo 3

Agora só nos resta resolver as integrais. No item (a), vamos calcular a integral em ϕ :

∫ 0 π 2 s e n   2 ϕ 2   d ϕ

A integral é:

- 1 4 cos ⁡ 2 ϕ 0 π 2

Aplicando os limites de integração temos:

= 1 2

Já em ρ :

∫ 0 a ρ 3   d ρ = ρ 4 4 0 a

Aplicando os limites de integração temos:

= a 4 4

Assim,

z - = 3 a 3 ⋅ a 4 4 ⋅ 1 2 = 3 a 8

Ou seja:

( 0,0 , 3 a 8 )

Passo 4

Neste passo vamos resolver a integral do item (b). Fazendo a integral em ρ :

I = δ a 5 5   ∫ 0 π / 2 ∫ 0 2 π s e n 3 ϕ cos 2 ⁡ θ + cos 2 ⁡ ϕ   s e n   ϕ   d θ   d ϕ

Lembrando que

∫ 0 2 π cos 2 ⁡ θ   d θ = 1 2 ∫ 0 2 �� 1 + cos ⁡ 2 θ   d θ = π ,

temos que

I = δ a 5 5   ∫ 0 π 2 π   s e n 3 ϕ + 2 π cos 2 ⁡ ϕ   s e n   ϕ   d ϕ

Assim,

I = π δ a 5 5   ∫ 0 π 2 1 - cos 2 ⁡ ϕ + 2 cos 2 ⁡ ϕ   s e n   ϕ   d ϕ

Então,

I = π δ a 5 5   ∫ 0 π 2 1 + cos 2 ⁡ ϕ   s e n   ϕ   d ϕ

Vamos fazer a mudança u = cos ⁡ ϕ , de modo que d u = - s e n   ϕ   d ϕ . Assim,

I = π δ a 5 5   ∫ 0 1 1 + u 2   d u = π δ a 5 5 1 + 1 3 = 4 15 π δ a 5

Resposta

a) 0 ,   0 , 3 a 8

b )   4 15 π δ a 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize coordenadas esféricas.Seja H um hemisfério sólido de raio a cuja densidade em qualquer ponto é proporcional à distância ao centro da base.a) Determine a massa de H .b) Determine o centro de ma
a) Determine o centroide de um cone circular reto com altura h e base com raio a. (Coloque o cone de forma que a base esteja sobre o plano x y com o centro na origem e seu eixo esteja sobre o eixo z.)
(a) Encontre o centroide do sólido no Exemplo 4 .(b) Encontre o momento de inércia em torno do eixo z para este sólido.
Determine os momentos de inércia para um cubo com densidade constante k e lados de comprimentoL se um vértice está localizado na origem e três arestas estão nos eixos coordenados.