Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 48
Escreva, mas não calcule, as expressões integrais para (a) a massa, (b) o centro de massa e (c) o momento de inércia em relação ao eixo .
O hemisfério ;
Passo 1
E ai, pessoal!
Nessa questão a gente precisa montar várias integrais, mas não calcular (que bom senão elas iam dar um trabalhinho 😂)
Bom, primeiro vamos relembrar as fórmulas dessas coisas que ele tá pedindo...
A gente tem a região , que é o hemisfério , e a função densidade
Com isso, a massa é calculada assim:
As coordenadas do centro de massa são:
E o momento de inércia em relação ao eixo :
A gente vai começar olhando pro nosso sólido , pra definir os limites de integração.
Com isso, vamos transformar essas integrais em integrais iteradas e pronto!
Passo 2
Nosso sólido é um hemisfério...
Tá, mas o que é isso??
É a metade de uma esfera! Nesse caso a esfera é de raio centrada na origem:
E esse hemisfério é a parte que :
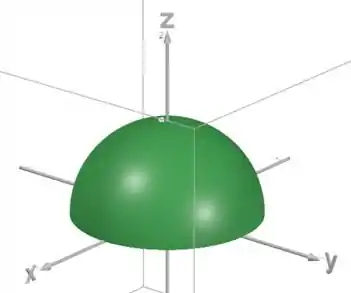
O sólido é limitado por cima pela superfície da esfera (ou seja, o do sólido vai ser menor que o da esfera)
Isolando :
Como estamos em :
Então achamos os limites de do sólido:
Passo 3
Para achar os limites de e , vamos olhar a projeção de no plano .
Ela é limitada por uma circunferência que é a interseção de
Ou seja, :
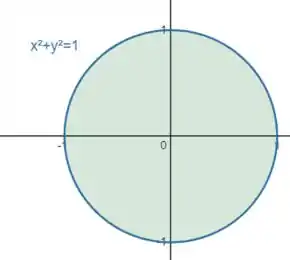
Se isolarmos o nessa expressão, vamos ter duas curvas:
A primeira é a parte de cima da circunferência e a segunda é a parte de baixo:
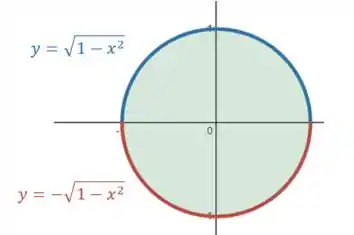
Como está entre essas duas curvas:
E o varia de até , então já temos todos os nossos limites:
Percebe que existe uma ordem certa pra integrarmos com esses limites.
Como depende das outras duas variáveis, vai ser o primeiro a ser integrado.
Depois , que depende de .
Por último, , já que seus limites são constantes.
Então, para uma função qualquer:
Agora vamos aplicar essa lógica nas nossas fórmulas!!
Passo 4
(a)
Para a massa, a fórmula é:
Então,
Passo 5
(b)
Para o centro de massa , calculamos:
Então:
Passo 6
(c)
Por último, o momento de inércia:
Fica:
Resposta
(a)
(b) onde:
(c)