Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 49

Seja E o sólido no primeiro octante limitado pelo cilindro x 2 + y 2 = 1 e pelos planos y = z , x = 0 e z = 0 com função densidade ρ x , y , z = 1 + x + y + z . Use um sistema de computação algébrica para determinar os valores exatos das seguintes quantidades para E .

  1. A massa
  2. O centro de massa
  3. O momento de inércia em relação ao eixo z

Passo 1

Fala, pessoal. Tudo show? 😊

A questão pede pra descobrir, através de programas, a (a) massa, o (b) o centro de massa e (c) o momento de inércia em relação a z do sólido E no primeiro octante, que está limitado pelo cilindro

x 2 + y 2 = 1

E pelos planos

y = z

x = 0

z = 0

Com função de densidade

ρ x , y , z = 1 + x + y + z

Sinistrooo!

Vamos começar descobrindo nossos limites de integração antes de tudo.

Através do cilindro podemos ter

x 2 + y 2 = 1

y 2 = 1 - x 2

y = ± 1 - x 2

Mas como estamos no primeiro octante, vamos utilizar somente a raiz positiva.

Além disso,

y = z

Mas z = 0 , então temos que:

0 ≤ y ≤ 1 - x 2

0 ≤ z ≤ y

E x = 0 também, por isso

x 2 + y ⏟ z = 0 2 = 1

x 2 = 1

x = ± 1

Também precisamos somente da raiz positiva:

0 ≤ x ≤ 1

Show de bolinhaaa! 😊

Passo 2

(a) A massa é dada por

m = ∭ E ρ   d V

Então substituindo pelo que já temos, vamos resolver:

m = ∫ 0 1 ∫ 0 1 - x 2 ∫ 0 y 1 + x + y + z   d z d y d x

Usando a calculadora do Responde Aí para computar esse valor temos

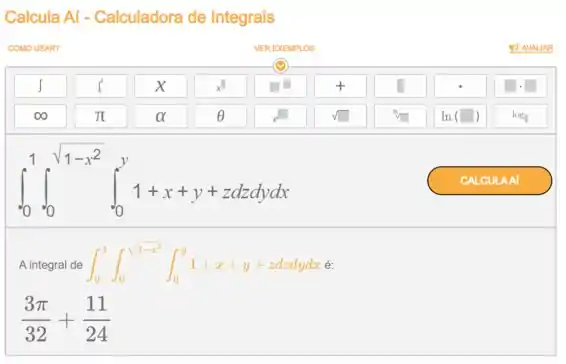
Ou melhor organizando, chegaremos a

m = 9 π + 44 96

Passo 3

(b) O centro de massa é dado por:

x - = 1 m ∭ E x   ρ   d V

y - = 1 m ∭ E y   ρ   d V

z - = 1 m ∭ E z   ρ   d V

Assim, substituindo, teremos:

x - = 1 m ∫ 0 1 ∫ 0 1 - x 2 ∫ 0 y x 1 + x + y + z   d z d y d x

x - = 1 m ⋅ 7 24

Sabemos que m = 9 π + 44 96 , então colocamos o inverso na fórmula:

x - = 96 9 π + 44 ⋅ 7 24 = 28 9 π + 44

Agora em y - :

y - = 1 m ∫ 0 1 ∫ 0 1 - x 2 ∫ 0 y y 1 + x + y + z   d z d y d x

y - = 1 m 15 π + 64 240

y - = 30 π + 128 45 π + 220

Agora em z - :

z - = 1 m ∫ 0 1 ∫ 0 1 - x 2 ∫ 0 y z 1 + x + y + z   d z d y d x

z - = 1 m 13 90 + π 32

z - = 208 + 45 π 135 π + 660

Passo 4

(c) Já o momento de inércia em relação ao eixo z é dado por essa fórmula aqui:

I z = ∭ E x 2 + y 2 ρ x , y , z   d V

Substituindo, teremos

I z = ∫ 0 1 ∫ 0 1 - x 2 ∫ 0 y ( x 2 + y 2 ) 1 + x + y + z   d z d y d x

E através de um software ou pela calculadora do Responde Aí, top demais, chegaremos a

I z = 17 60 + π 16

Moleza, né? 😉

Resposta

  1. m = 9 π + 44 96

  2. 28 9 π + 44 , 30 π + 128 45 π + 220 , 208 + 45 π 135 π + 660

I z = 17 60 + π 16

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia para um cubo com comprimento do lado L se um vértice está localizado na origem e três arestas estão nos eixos coordena
Suponha que o sólido tenha densidade constante k .Encontre o momento de inércia em relação ao eixo z do cilindro sólido x 2 + y 2 ≤ a 2 , 0 ≤ z ≤ h .
Suponha que o sólido tenha densidade constante k .Encontre os momentos de inércia de um tijolo retangular com dimensões a ,b e c e massa M se o centro do tijolo está localizado na origem e as arestas
Momento de inércia de um cone sólido Encontre o momento de inércia de um cone circular reto com raio de base ae altura h em relação ao seu eixo. (Sugestão: situe o cone comseu vértice na origem e seu
Momento de inércia de um cone sólido Encontre o momento de inércia de um cone circular reto com raio de base 1e altura 1 em relação ao eixo passando pelo vértice paralelo àbase. (Tome d = 1.)