Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 21
21. Calcular onde R é delimitada pelo triângulo de vértices
Passo 1
Temos a seguinte representação gráfica:
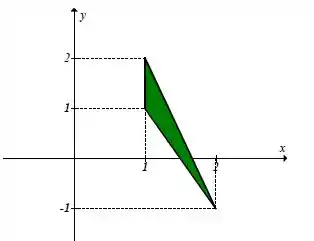
Analisando o gráfico temos os seguintes intervalos de integração:
Primeiro iremos integrar em relação a ,
Passo 2
Vamos separar os valores e resolver um por vez e em seguida somar os valores.
Passo 3
Das integrais anteriores as duas de segundo grau precisam ser resolvidas pelo método da substituição, assim:
Vamos chamar,
Dessa forma, temos:
Passo 4
Das integrais anteriores as duas de segundo grau precisam ser resolvidas pelo método da substituição, assim:
Vamos chamar,
Dessa forma, temos:
Passo 5
Ao juntar as integrais iniciais, temos:
Resposta
Exercícios de Livros Relacionados
Mostrar que as regiões R 1eR 2 , têm a mesma área
Calcular a área região delimitada pela curva x 2 3 + y 2 3 = 1
Calcular a área da região do 1º quadrante delimitada pelas curvas y 2 = 8 a x , x + y = 6 a , y = 0 , sendo a uma constante positiva.
Calcular a área da elipse x 2 + 4 y 2 - 4 x = 0 .
Calcule ∫ ∫ B y d x d y onde B é o conjunto dado.