Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.7 - Ex. 6
Calcular , onde T é a região interior às superfícies e
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar:
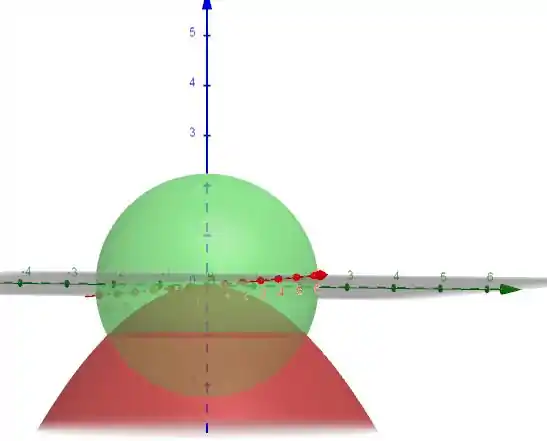
O nosso cilindro é delimitado superiormente pelo paraboloide e inferiormente pela equação da esfera, certo?
Então z estará entre:
E:
Sendo assim, em coordenadas cilíndricas para facilitar a integral:
Agora nós precisamos analisar onde as duas superfícies se interceptam para pormos achar o raio, ok?
Da equação do paraboloide:
Colocando na equação da esfera:
Resolvendo a equação de segundo grau:
Pelo desenho nós vemos que elas se encontram quando , substituindo em uma das equações em coordenadas cilíndricas:
Sendo assim,
Só falta nós acharmos o ângulo, mas como ambos fazem uma volta completa:
Passo 2
Agora que já sabemos os intervalos de integração, podemos usar a definição (4) para mudar as variáveis de integração:
Resolvendo:
Sendo assim:
Aplicando na integral:
Resolvendo a integral:
Aplicando o intervalo:
Passo 3
Agora vamos colocar o resultado do passo 2 na equação:
Aplicando o intervalo:
Gostaram dessa?