Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.7 - Ex. 20
Calcular , onde T é a região limitada por , e
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar:
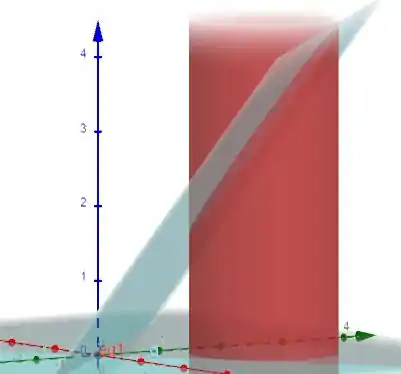
Para resolver este tipo de questão nós vamos fazer uma mudança de variáveis:
Colocando na fórmula do cilindro:
Desenhando:
O nosso cilindro é limitado por
Já sabemos que o intervalo de z será:
Para o u e o v basta usarmos o cilindro, certo?
Então v estará entre:
Legal, agora só precisamos de u Que obrigatoriamente deverá ser:
Ou melhor:
Passo 2
Agora que já sabemos os intervalos de integração:
Resolvendo:
Aplicando na integral:
Agora vamos resolver a segunda:
Aplicando o intervalo:
E aplicamos na última integral:
Passo 3
Agora vamos resolver cada termo separadamente:
Chamando:
O novo intervalo será:
Então:
Usando a identidade:
Lembrando que:
Então:
Usando uma substituição simples:
Aplicando o intervalo:
Passo 4
Na segunda integral:
Aqui nós vamos resolver por partes:
Como nossa integral ficará?
Pelo Passo 3 sabemos que:
Substituindo o resultado e o intervalo:
Sendo assim:
Passo 5
Na última integral:
Chamando:
O novo intervalo será:
Então:
Usamos a identidade novamente:
Usando:
Então:
Por substituição:
No intervalo:
Aplicando na integral do Passo 2:
E terminamos mais umaa !