Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.7 - Ex. 4

Calcular ∭_T^() d V , onde T é a região limitada por x^2 + y^2 - x = 0 e x^2 + y^2 + z^2 = 1 .

Passo 1

Bora começar?!

Então galera, a primeira coisa a fazer aqui é tentar desenhar:

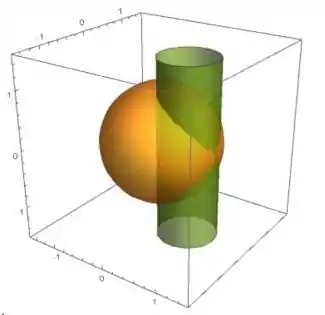
O nosso cilindro é delimitado superiormente e inferiormente pela equação da esfera, certo?

Então:

x^2 + y^2 + z^2 = 1

z = +- sqrt(1 - ( x^2 + y^2 ))

Transformando em coordenadas cilíndricas:

z = +- sqrt(1 - r^2)

Belezaaa! Agora que já sabemos a variação da altura só precisamos achar a área, que é definida pelo plano xy.

Nós podemos expressar o raio também em coordenadas cilíndricas:

r = cos theta

Então:

0 <= r <= cos theta

Para que o raio seja positivo o nosso ângulo deverá estar no intervalo:

- (pi)/(2) <= theta <= (pi)/(2)

Passo 2

Agora que já sabemos os intervalos de integração, podemos usar a definição (4) para mudar as variáveis de integração:

∭_T^() d V = ∬_R^() [int_(- sqrt(1 - r^2))^(sqrt(1 - r^2)) d z] r d r d theta

Resolvendo:

int_(- sqrt(1 - r^2))^(sqrt(1 - r^2)) d z = z = (sqrt(1 - r^2) - ( - sqrt(1 - r^2) ))

= 2 sqrt(1 - r^2)

Sendo assim:

= ∬_R^() 2 r sqrt(1 - r^2) d r d theta

= r ∬_R^() r sqrt(1 - r^2) d r d theta

Aplicando na integral:

= 2 int_(- (pi)/(2))^((pi)/(2)) [ int_0^(cos theta) r sqrt(1 - r^2) . d r ] d theta

Resolvendo a integral:

int_0^(cos theta) r sqrt(1 - r^2) . d r

Vamos chamar:

u = sqrt(1 - r^2)

d u = (1)/(2) . - 2 r . (1 - r^2)^(- (1)/(2)) d r = - (r d r)/(sqrt(1 - r^2)) = - (r d r)/(u) -> r d r = - u d u

Substituindo:

int_0^(cos theta) u . ( - u d u ) = - int_0^(cos theta) u^2 . d u = - (u^3)/(3)

Voltando ao u:

- (u^3)/(3) = - (1)/(3) (1 - r^2)^((3)/(2))

Agora aplicamos o intervalo:

= - (1)/(3) [ (1 - cos^2 theta)^((3)/(2)) - 1 ]

Pela identidade:

= - (1)/(3) [ (sen theta^2)^((3)/(2)) - 1 ]

= - (1)/(3) [ |sen theta|^3 - 1 ]

= (1)/(3) [ 1 - |sen theta|^3 ]

Passo 3

Agora vamos colocar o resultado do passo 2 na equação:

= 2 int_(- (pi)/(2))^((pi)/(2)) (1)/(3) [ 1 - |sen theta|^3 ] d theta

= (2)/(3) int_(- (pi)/(2))^((pi)/(2)) [ 1 - |sen theta|^3 ] d theta

Podemos reorganizar esta integral para facilitar:

= (4)/(3) int_0^((pi)/(2)) [ 1 - sen^3 ( theta ) ] d theta

= (4)/(3) [int_0^((pi)/(2)) d theta - int_0^((pi)/(2)) sen^3 (theta) d theta]

= (4)/(3) [int_0^((pi)/(2)) d theta - int_0^((pi)/(2)) sen^2 (theta) . s e n (theta) d theta]

= (4)/(3) [theta - int_0^((pi)/(2)) sen^2 (theta) . s e n (theta) d theta]

Pela identidade:

= (4)/(3) [int_0^((pi)/(2)) d theta - int_0^((pi)/(2)) ( 1 - cos^2 (theta) ) . s e n (theta) d theta]

Chamando:

u = cos (theta)

d u = - s e n (theta) . d theta

= (4)/(3) [theta + int_0^((pi)/(2)) ( 1 - u^2 ) d u]

= (4)/(3) [theta + int_0^((pi)/(2)) d u - int_0^((pi)/(2)) u^2 d u]

= (4)/(3) [theta + u - (u^3)/(3)]

Substituímos o u:

= (4)/(3) [theta + cos (theta) - (cos^3 (theta))/(3)]

E aplicando o intervalo:

= (4)/(3) [(pi)/(2) + (0 - 1) - (( 0 - 1 ))/(3)]

= (4)/(3) [(pi)/(2) - 1 + (1)/(3)] = (4)/(3) xx (3 pi - 4)/(6)

= (2)/(9) ( 3 pi - 4 )

Ufaaa !!

Acabamos mais uma !

Resposta

(2)/(9) ( 3 pi - 4 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o sólido descrito pelas desigualdades dadas. 0 ≤ r ≤ 2 ,- π 2 ≤ θ ≤ π 2 ,0 ≤ z ≤ 1
Utilize coordenadas cilíndricas.Determine a massa e o centro de massa do sólido S delimitado pelo paraboloide z = 4 x 2 + 4 y 2 e pelo plano z = a( a0 ) , se S tem densidade constante K .
Utilize coordenadas cilíndricas.Ache o volume da região E limitada pelo paraboloide z = 24 - x 2 - y 2 e o cone z = 2 x 2 + y 2 .Encontre o centroide do E (centro de massa no caso em que a densidade é
Calcule a integral, transformando para coordenadas cilíndricas. ∫ - 2 2 ∫ - 4 - y 2 4 - y 2 ∫ x 2 + y 2 2 x zd z d x d y
Calcule a integral, transformando para coordenadas cilíndricas. ∫ - 3 3 ∫ 0 9 - x 2 ∫ 0 9 - x 2 - y 2 x 2 + y 2d z d y d x