Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 27

Utilize coordenadas cilíndricas.

Determine a massa e o centro de massa do sólido S delimitado pelo paraboloide z = 4 x 2 + 4 y 2 e pelo plano z = a   ( a > 0 ) , se S tem densidade constante K .

Passo 1

Vamos lá pessoal. Temos um sóllido S limitado pelo paraboloide z = 4 x 2 + 4 y 2 e pelo plano z = a   a > 0 e temos que calcular seu centro de massa, e massa. Veja que a coordenada z está em função de 4 ( x 2 + y 2 ) . Isso significa que faz sentido pensarmos em passar para coordenadas polares pois facilitará os cálculos.

Dito isso, vamos recordar como que faz os cálculos solicitados?

A massa é:

m = ∭ E ρ   d V

O centro de massa é:

x - = 1 m ∭ E x   ρ   d V

Passo 2

O paraboloide z = 4 x 2 + 4 y 2 intercepta o plano z = a quando

a = 4 x 2 + 4 y 2

a = 4 ( x 2 + y 2 )

Vamos recordar da regrinha de transformação polar?

x 2 + y 2 = r 2

Dito isso, podemos escrever:

a = 4 ( r 2 )

Escrevendo em função de r :

a 4 = r 2

, e temos que r = 1 2 a .

Assim, a região de integração é dada por coordenadas cilíndricas:

E = r , θ , z | 0 ≤ θ ≤ 2 π ,   0 ≤ r ≤ 1 2 a , 4 r 2 ≤ z ≤ a

Temos que a massa é:

m = K ∙ V = K ∫ 0 2 π ∫ 0 1 2 a ∫ 4 r 2 a r d z d r d θ

Onde K é a densidade e V o volume.

Passo 3

Vamos resolver a integral:

m = K ∫ 0 2 π ∫ 0 1 2 a ∫ 4 r 2 a r d z d r d θ

Começando pela integral “mais interna”:

= K ∫ 0 2 π ∫ 0 1 2 a r z 4 r 2 a d r d θ

Substituindo os limites de integração, simplificando:

K ∫ 0 2 π ∫ 0 1 2 a r a - 4 r 2 r d r d θ = K ∫ 0 2 π ∫ 0 1 2 a r a - 4 r 3 d r d θ

Integrando em relação a r

K ∫ 0 2 π r 2 a 2 - r 4 0 1 2 a d θ = K ∫ 0 2 π 1 2 a 2 a 2 - 1 2 a 4 - 0 2 a 2 - 0 4 d θ

Simplificando:

K ∫ 0 2 π a 2 8 - a 2 16 d θ = K ∫ 0 2 π a 2 16 d θ

Resolvendo em função de θ

K a 2 16 θ 0 2 π = K a 2 16 2 π - a 2 16 0 = a 2 π K 8

Passo 4

Vamos agora achar o centro de massa. Veja que o sólido é simétrico em relação aos planmos x y e x z . Podemos tentar imaginar esse sólido. Veja:

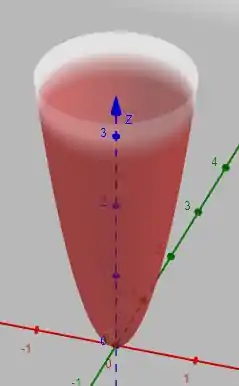
Temos por simetria que:

M y z = M x z = 0

O centro de massa é:

x - = 1 m ∭ E x   ρ   d V

Sendo que está relacionado a coordenada de cálculo:

Só nos resta calcular M x y :

M x y = ∫ 0 2 π ∫ 0 1 2 a ∫ 4 r 2 a K r z d z d r d θ

Resolvendo a integral “mais interna”

= K ∫ 0 2 π ∫ 0 1 2 a r z 2 2 4 r 2 a d r d θ

Aplciando limites e simplificando:

= K ∫ 0 2 π ∫ 0 1 2 a r a 2 2 - r 4 r 2 2 2 d r d θ = K ∫ 0 2 π ∫ 0 1 2 a r a 2 2 - 8 r 5 d r d θ

Resolvendo integral em função de d r

= K ∫ 0 2 π r a 2 2 4 - 4 r 6 3 0 1 2 a d θ = K ∫ 0 2 π 1 2 a a 2 2 4 - 4 1 2 a 6 3 - 0 a 2 2 4 - 4 . 0 6 3 d θ

Simplificando e fazendo a integral em função de θ

= K ∫ 0 2 π a 3 24 d θ = K a 3 24 θ 0 2 π = K a 3 24 2 π - a 3 24 0 = a 3 π K 12

Temos então que:

z - = M x y m = a 3 π K 12 a 2 π K 8 = a 3 π K 12 ∙ 8 a 2 π K = 2 a 3

Assim, o centro de massa é:

x - , y - , z - = 0,0 , 2 a 3  

Resposta

m = a 2 π K 8

x - , y - , z - = 0,0 , 2 a 3  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize coordenadas cilíndricas.Determine o volume do sólido que o cilindro r = a cos ⁡ θ corta da esfera de raio a centrada na origem.Ilustre o sólido da parte (a) desenhando a esfera e o cilindro na
Uma casca cilíndrica tem 20 cm de comprimento, com raio interno 6 cm e raio extreno 7 cm. Escreva desigualdades que descrevam a casca em um sistema de coordenadas adequado. Explique como você posicion
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral. ∫ 0 4 ∫ 0 2 π ∫ r 4 r d z d θ d r
Utilize coordenadas cilíndricas.Determine o volume do sólido que está dentro tanto do cilindro x ² + y ² = 1 ² ² como da esfera x ² + y ² + z ² = 4 ² ² ² .
Utilize coordenadas cilíndricas.Ache o volume da região E limitada pelos paraboloides z = x 2 + y 2 e z = 36 - 3 x 2 - 3 y 2 .Encontre o centroide do E (centro de massa no caso em que a densidade é co