Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.8 - Ex. 11
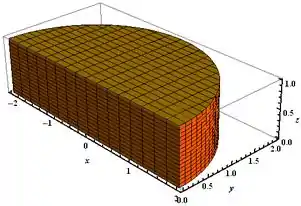
Esboce o sólido descrito pelas desigualdades dadas.
Passo 1
Fala, meus amigos! Tranquilidade?
A questão quer que a gente esboce o sólido que é descrito por:
Bom, como temos uma região em função de , o que temos aqui é uma região descrita em coordenadas cilíndricas.
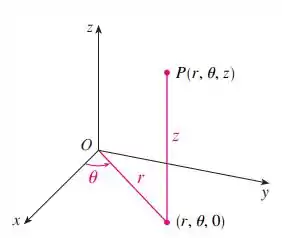
Esquema de representação de um ponto em coordenadas esféricas
Então, vamos analisar variável por variável, achar o comportamento de cada uma e entender qual sólido cada uma dessas variações vão formar.
Vamos lá!
Passo 2
Vamos entender a variação de cada variável no espaço.
Essa informação nos diz que temos uma circunferência de raio .
Essa informação nos diz que essa circunferência não é completa. Só temos metade dela, indo de até
Essa informação, já é sobre a altura do cilindro, que ocupa do o eixo e tem altura igual a .
Partiu esboçar o gráfico agora...
Passo 3
Juntando as informações acima, nosso sólido deve ser metade de uma circunferência de raio , somente a metade positiva do eixo , com altura variando de 0 até .
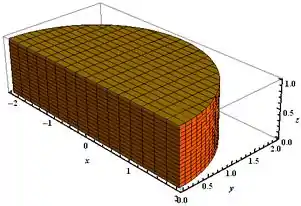
Resposta
