Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 10
Calcular o volume da parte da esfera entre os planos e .
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar, certo?
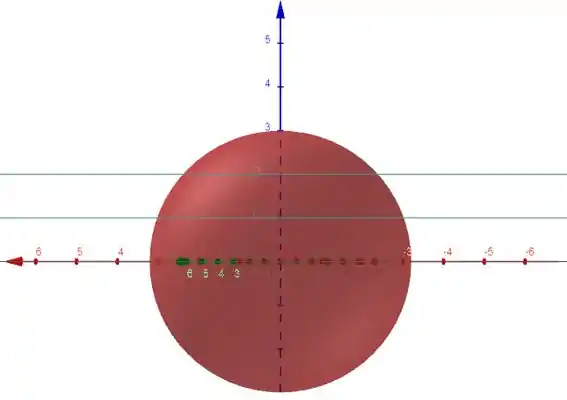
Então, o que faremos?
Vamos calcular o volume da semiesfera de 1 até o topo e subtrair do volume da semiesfera que vai de 2 até o topo
Em coordenadas esféricas:
O raio é delimitado pelos valores de z. Quando
O maior raio é obtido quando
O é o ângulo que o ponto pode fazer com o eixo x, na esfera esse ângulo vai de 0 até 360°:
Passo 2
Agora que já sabemos os intervalos de integração:
Resolvendo a primeira integral:
Sendo assim:
Vamos primeiro resolver a integral e depois aplicar os intervalos para cada uma separadamente:
Agora vamos chamar:
De volta ao r:
Aplicando o intervalo:
Agora vamos lançar na integral:
Então:
Passo 3
A próxima integral é:
De maneira similar ao anterior:
Agora vamos lançar na integral:
Então:
Se o volume da nossa figura é:
Substituindo pelos resultados:
O que acharam desta??