Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 7
Calcular o volume do sólido acima do plano xy e interior às superfícies e
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar, certo?
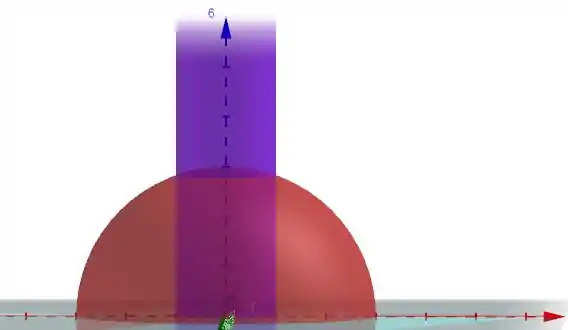
Para calcular o volume nós vamos precisar limitar z.
Sabemos que o volume que queremos está no interior de ambas as figuras dadas e limitada pelo plano xy, certo?
Então, o z deverá estar entre:
Em coordenadas cilíndricas:
Então:
Para definir o r nós precisamos olhar atentamente para a figura e perceber que o cilindro irá definir o raio, então:
Sendo assim:
O é o ângulo que o ponto pode fazer com o eixo x, na esfera esse ângulo vai de 0 até 360°:
Passo 2
Agora que já sabemos os intervalos de integração:
Resolvendo:
Sendo assim:
Resolvendo a integral:
Vamos chamar:
Substituindo u:
Aplicando o intervalo:
Então:
Finalizamos mais umaa !!