Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 12

Nos exercícios 11 a 19, calcular o volume do sólido delimitado pelas superfícies dadas.

12. x 2 + 2 y 2 = 2 ; z = 0 e z = x + 4 .

Passo 1

Bora começar?!

Então galera, a primeira coisa a fazer aqui é tentar desenhar, certo?

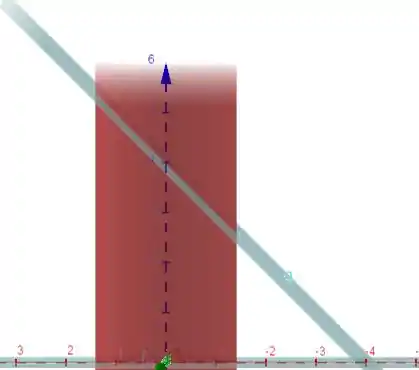
Beleza galera !!

Pelo desenho tá fácil, não está?! O z é delimitado por z = 0 e z = x + 4 .

Então:

0 ≤ z ≤ x + 4

O valor de x nós podemos delimitar usando o cilindro:

x 2 + 2 y 2 = 2

x 2 = 2 - 2 y 2

x = ± 2 - 2 y 2

Então:

- 2 - 2 y 2 ≤ x ≤ 2 - 2 y 2

Para o y basta nós lembrarmos que:

2 - 2 y 2 ≥ 0

y = ± 1

Ou melhor:

- 1 ≤ y ≤ 1

Passo 2

Agora que já sabemos os intervalos de integração:

∭ T d V = ∫ 1 1 ∫ - 2 - 2 y 2 2 - 2 y 2 ∫ 0 x + 4 d z d x d y

Resolvendo a primeira integral:

∫ 0 x + 4 d z = z = x + 4

Sendo assim:

= ∫ 1 1 ∫ - 2 - 2 y 2 2 - 2 y 2 x + 4 d x d y

Nesta segunda integral teremos:

∫ - 2 - 2 y 2 2 - 2 y 2 x + 4 d x = x 2 2 + 4 x = 1 2 2 - 2 y 2 2 - - 2 - 2 y 2 2 + 4 ( 2 2 - 2 y 2 )

= 8 2 - 2 y 2

Passo 3

Substituindo na última integral:

= ∫ 1 1 8 2 - 2 y 2 d y

Para resolver vamos chamar:

y = s e n   ( u )

d y = cos ⁡ ( u ) . d u

O novo intervalo será:

u = π 2

u = - π 2

= ∫ - π 2 π 2 8 2 - 2 s e n 2 u ( cos ⁡ ( u ) . d u )

= ∫ - π 2 π 2 8 2 ( 1 - s e n 2 u ) ( cos ⁡ ( u ) . d u )

Conhecendo a identidade:

= ∫ - π 2 π 2 8 2 c o s 2 u ( cos ⁡ ( u ) . d u )

= 8 2 ∫ - π 2 π 2 cos 2 ⁡ ( u ) . d u

Sabendo que:

cos 2 ⁡ ( u ) = 1 + cos ⁡ ( 2 u ) 2

Na integral:

= 4 2 ∫ - π 2 π 2 ( 1 + cos ⁡ ( 2 u ) ) . d u

Resolvendo por uma substituição simples:

= 4 2 u + 1 2 s e n   2 u

No intervalo:

= 4 2 π + 1 2 s e n   π - s e n   - π

= 4 π 2

Gostaram ?!

Resposta

4 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam B ⊂ R 3 e f x , y , z uma função contínua em B . Seja ( x 0 , y 0 , z 0 ) um ponto interior de B . Para cada natural n , seja B n uma bola de centro x 0 , y 0 , z 0 e raio r n , com B n ⊂ B . Su
Encontre o valor médio da função ƒ(r, f, u) = r cos f sobre asemiesfera sólida r ≤ 1, 0 ≤ f ≤ p/2.
Encontre o valor médio da função ƒ(r, f, u) = r sobre a esferasólida r ≤ 1.
Encontre o valor médio da função ƒ(r, u, z) = r sobre a regiãodelimitada pelo cilindro r = 1 entre os planos z = –1 e z = 1
Centro de massa Um sólido de densidade constante é delimitado abaixo pelo plano z = 0, acima pelo cone z = r, r ≥ 0,e dos lados pelo cilindro r = 1. Encontre o centro de massa.