Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.9 - Ex. 2
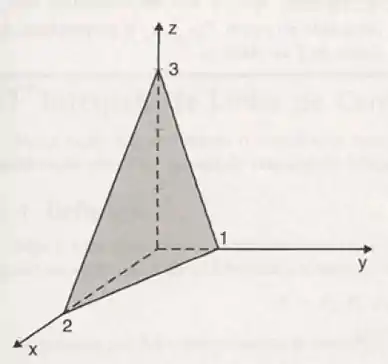
Calcular o volume do tetraedro da Figura 8.32.
- Entre os planos e ;
- Acima do plano
- Abaixo do plano
Passo 1
Então galera, já sabemos que a equação do plano é:
Também já sabemos que z é limitada pelo um e pelo dois:
Analisando o y nós vemos que:
Então:
Agora nós precisamos relaciona o x com z, quando :
Concluindo:
Como fica nossa integral ? Fácil !!
Começando pela primeira integral:
Então:
Agora vamos resolver a segunda integral:
Aplicando o intervalo:
Na última integral:
No intervalo:
Passo 2
No segundo tópico nós queremos o volume da parte acima do plano ou melhor:
Então a integral ficará:
Como nós só mudamos o intervalo da última integral, as outras apresentam o mesmo resultado:
No intervalo:
Passo 3
No terceiro tópico nós queremos o volume da parte abaixo do plano ou melhor:
Então a integral ficará:
Como nós só mudamos o intervalo da última integral, as outras apresentam o mesmo resultado:
No intervalo:
Finalizamos mais umaa !!