Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.7 - Ex. 23
Use a Regra do Ponto Médio para as integrais triplas (Exercício 24) para estimar o valor da integral. Divida em oito subcaixas de igual tamanho.
onde
Passo 1
Fala turminha, tudo na paz?
Precisamos usar a regra do ponto médio para integrais triplas e estimar o valor da integral a baixo:
Dividindo em oito subcaixas de igual tamanho. Onde é definido como:
Vish, como resolvo essa?
Calma! Vamos lembrar a regra do ponto médio em integrais triplas primeiro.
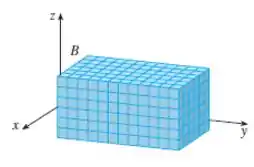
Onde, .
Observe que temos uma figura tridimensional, e é feita uma aproximação da integral tripla a partir de um somatório.
Como ele forneceu no enunciado que quer dividir em subcaixas, temos que .
Nosso objetivo é determinar os pontos médios de cada uma dessas subcaixas.
Feito isso, precisamos aplicar na função do somatório expandido, e multiplicar por .
Bora lá resolver essas juntos?
Passo 2
Precisamos dividir em oito subcaixas de igual tamanho, certo?
é definido como:
Observe como fica isso graficamente:
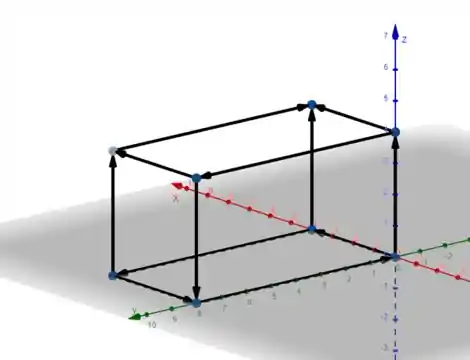
Mas lembre-se que precisamos de 8 caixas iguais. Logo, basta dividirmos cada intervalo no meio e pegar os pontos médios destes intervalos.
Se dividirmos todas as variações em duas, ficamos com:
Para :
e
Para temos a mesma variação,
e
Já para vamos ter:
e
Vamos ver como fica nosso sólido dividido em oito subcaixas:
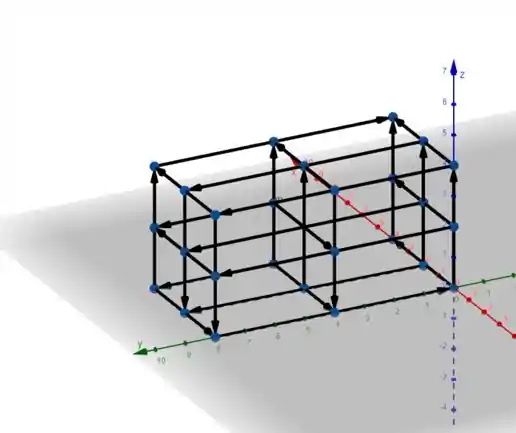
Vamos precisar determinar os pontos médios das oito caixas, e com a figura ficou fácil.
Analisando os pontos médios de cada subcaixa, ficamos com os pontos
Passo 3
Para estimar a integral, pegamos o volume de cada caixa que é .
Pelo valor da função no ponto médio da caixa, então temos
Comparando com a integral dada:
Sabemos que:
Logo, nosso volume pela regra do ponto médio vai ficar:
Aplicando cada ponto na função acima, temos: