Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 12.4 - Ex. 1m
Calcule
Passo 1
Oi, pessoal! Na integral que temos para resolver tem um polinômio de grau dois dentro de uma raíz. Isso tem cara que da para simplificar né? Vamos reescrever esse polinômio para ver se simplifica!
Essa raíz é muito diferente do que estamos acostumados, mas podemos modelar para algo:
O nosso objetivo era transformar em algo do tipo, pois assim podemos fazer uma substituição trigonométrica:
Porém essa equação tá muito estranha e nem dá pra colocar em algum formato que possamos resolver, porém essa equação quase é: , e se somarmos 1?
Claro, temos que subtrair 1 também pra manter a raíz original, então:
Agora estamos perto dessa forma
Para ficar nesse formato vamos aceitar que e que , então teremos:
A função dentro da integral é:
Pronto! Agora podemos fazer a nossa substituição trigonométrica!
Passo 2
A substituição trigonométrica funciona assim!
A gente pega um triângulo retângulo com ângulo como esse:
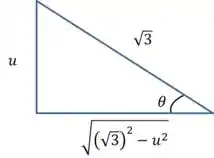
Agora vamos para substituição!
Bem, se dissermos que
Então,
Derivando o seno,
Assim podemos substituir a integral dessa forma:
Ótimo! Agora podemos calcular essa integral de maneira mais fácil
Passo 3
Podemos, agora, integrar:
Lembrando que:
Se fizermos a substituição:
Então:
Voltando pra variável :
Mas ainda não acabou! Temos que chegar na variável
Passo 4
Vamos lembrar que:
Então o nosso será,
E que:
Assim:
Temos que voltar pra variável ! Lembra que,
Temos, então: