Calcule a área do conjunto dado.
- é o conjunto do plano limitado pela reta e pelos gráficos de e , com
Passo 1
- Vamos fazer o gráfico da região da integração:
- Vamos fazer o gráfico da região da integração:
- Vamos fazer o gráfico da região da integração:
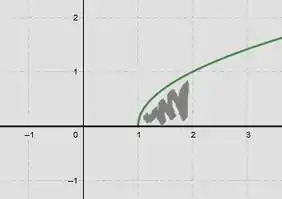
Temos então que a área do conjunto dado é a integral com os limites de integração e integrando com a função de cima do gráfico menos a de baixo:
Passo 2
Bem, aqui vamos usar a Regra da Substituição, então mãos a massa, vamos fazer uma mudança de variável para encontrar o valor dessa integral:
Vamos agora achar diferencial de , derivando:
E temos que os novos limites de integração vão ser:
Vamos agora fazer a substituição:
Agora fica simples de resolver, vamos lá.
Passo 3
Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Agora é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:
Agora é só aplicar:
Pronto, já encontramos a integral indefinida, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Ficamos então com:
Passo 4
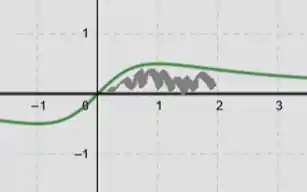
Temos então que a área do conjunto dado é a integral com os limites de integração e integrando com a função de cima do gráfico menos a de baixo:
Passo 5
Bem, aqui vamos usar a Regra da Substituição, então mãos a massa, vamos fazer uma mudança de variável para encontrar o valor dessa integral:
Vamos agora achar diferencial de , derivando:
E temos que os novos limites de integração vão ser:
Vamos agora fazer a substituição:
Agora fica simples de resolver, vamos lá.
Passo 6
Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Agora é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:
Agora é só aplicar:
Passo 7
Pronto, já encontramos a integral indefinida, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Ficamos então com:
Passo 8
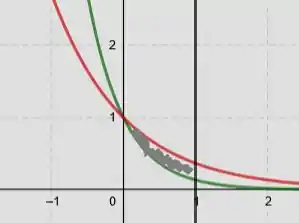
Temos então que a área do conjunto dado é a integral com os limites de integração e integrando com a função de cima do gráfico menos a de baixo:
Passo 2
Bem, aqui vamos usar a Regra da Substituição, então mãos a massa, vamos fazer uma mudança de variável para encontrar o valor dessa integral:
Vamos agora achar diferencial de , derivando:
E temos que os novos limites de integração vão ser:
Vamos agora fazer a substituição:
Com a segunda vamos fazer:
Vamos agora achar diferencial de , derivando:
E temos que os novos limites de integração vão ser:
Vamos agora fazer a substituição:
Agora fica simples de resolver, vamos lá.
Passo 3
Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Agora é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:
Agora é só aplicar:
Passo 4
Pronto, já encontramos a integral indefinida, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Ficamos então com: