Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 4d
Calcule a área de interseção da região limitada pelas curvas:
Passo 1
Antes de começarmos o desenvolvimento, temos que prestar atenção no domínio das funções, visto que devido a raiz quadrada, só podemos pegar intervalos de seno e cosseno positivos (primeiro quadrante). Além disso, só podemos trabalhar com o raio positivo.
Primeiramente, vamos igualar as funções para descobrir o ponto de interseção entre elas:
Sabemos que satisfaz a equação acima
Passo 2
Para facilitar a vizualização, vizualizaremos os gráficos superpostos.
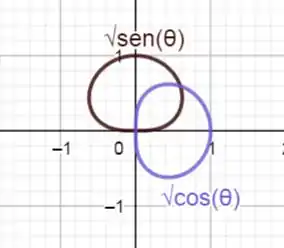
Podemos notar que a área entre os gráficos é a área do gráfico roxo de até mais a área do gráfico preto de 0 até
Passo 3
Sabemos que a fórmula para a área em coordenadas polares é:
0,5
Aplicando os limites de integração:
+ 0,5
Resolvendo a integral simples:
+ 0,5 = 1 -
Resposta
A área vale 1 -