Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 6

Calcule a área de interseção da região limitada pelas curvas no primeiro quadrante:

x4 – y4 = 2xy

ρ =   √ 2 s e n ( 2 θ )

Passo 1

Primeiramente, vamos passar a primeira equação para coordenadas polares:

Primeiramente, sabemos que:

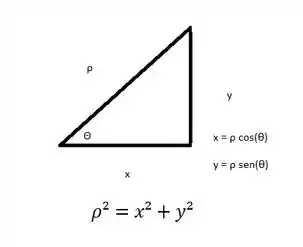
Logo, na primeira parcela:

X4 – y4 = (x² + y²) (x² - y²) = ρ 2 ρ 2 c o s 2 θ - ρ 2 s e n 2 θ = ρ 4 (cos²( θ ) - s e n ² ( θ ) )

Sabemos que cos²( θ ) - s e n ² ( θ ) = cos( 2 θ ) , e portanto X4 – y4 = ρ 4 cos( 2 θ )

Do outro lado, temos que 2xy = 2 ρ 2 s e n θ c o s ⁡ ( θ )

Sabemos que 2   s e n θ c o s ⁡ ( θ ) = sen(2 θ ) e portanto, 2xy = 2 ρ 2 s e n θ c o s ⁡ ( θ ) = ρ 2 sen(2 θ )

Igualando as equações, temos que:

ρ 2 sen(2 θ ) = ρ 4 cos( 2 θ )

Logo: ρ 2 = t g ( 2 θ )

ρ = √   t g ( 2 θ )

Passo 2

Em segundo lugar, devemos igualar as funções para achar o ponto de interseção:

√   t g ( 2 θ ) =   √ 2 s e n ( 2 θ )

t g 2 θ =   2 s e n 2 θ

2 s e n 2 θ = s e n 2 θ cos ⁡ 2 θ

2 = 1/cos(2 θ )

cos(2 θ ) = 1 2

Temos que os valores de θ = π 6 e θ = 5 π 6 satisfazem a equação acima, entretanto, nós queremos só no primeiro quadrante e então descartamos o segundo resultado.

Passo 3

Para facilitar a vizualização, vizualizaremos os gráficos superpostos.

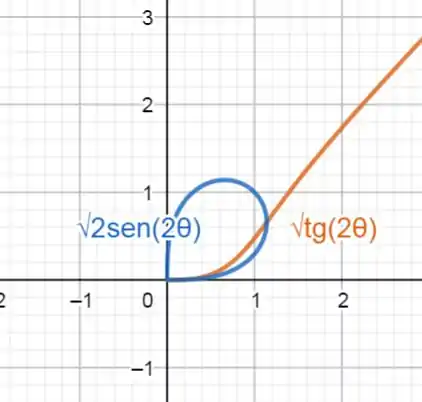
Podemos ver que a área entre as curvas é a área da curva azul menos a área da curva laranja, ambas no intervalo de 0 até π 6 .

Passo 4

Sabemos que a fórmula para a área em coordenadas polares é:

0,5 ∫ a b ρ ² d θ

Aplicando os limites de integração:

1 2 ∫ 0 π / 6 2 s e n ( 2 θ ) d θ -   1 2 ∫ 0 π / 6 t g ( 2 θ ) d θ = 1 4 - ln ⁡ 2 4

Resposta

A área vale 1 4 - ln ⁡ 2 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área da região dada (coordenadas polares): ρ ² = cos ⁡ θ( p ≥ 0 ) ²
Calcule a área limitada pela curva (coordenadas polares) : ρ = 2 - c o s ⁡ ( θ )
Escreva, em coordenadas polares, a equação da elipse x 2 a 2 + y 2 b 2 = 1 , tomando como pólo o foco F=( c , 0 ) ,c0 , e como eixo polar a semi-reta F A onde A = ( a , 0 ) ,a0 . Faça e = c a e ρ = a
Calcule a área de interseção da região limitada pelas curvas: ρ = 3 ρ = 2 - 2 c o s ⁡ ( θ )
Calcule a área do conjunto de todos os pontos ( θ , ρ ) tais que θ ²≤ ρ ≤ θ ²