Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.4 - Ex. 4c

Calcule a área das seguintes superfícies

c) Superfície do sólido limitado pelo cone z 2 = x 2 + y 2 e a parte superior da esfera x 2 + y 2 + z 2 = 1 .

Passo 1

Veja a figura abaixo:

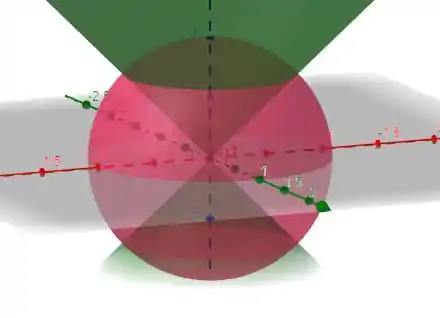
A área que desejamos é a superfície lateral do cone que está no interior da esfera (vamos chamar de A 1 ) e a calota esférica superior (vamos chamar de A 2 )

Passo 2

Vamos começar calculando A 1 .

Uma parametrização imediata para o nosso cone é tomarmos:

φ x , y = x ,   y ,   x 2 + y 2

Como desejamos a parte superior da esfera, vamos nos preocupar apenas com z ≥ 0 . Note que

x 2 + y 2 + z 2 = 1 x 2 + y 2 + x 2 + y 2 = 1 2 x 2 + y 2 = 1 x 2 + y 2 = 1 2

ou seja, x , y está no interior de um círculo de centro 0 ,   0 e raio 1 / 2 .

Passo 3

A área A 1 é dada por:

A 1 = ∬ D ∂ φ ∂ x × ∂ φ ∂ y   d x   d y

Note que as derivadas são exatamente iguais a do item b). Assim, usando o resultado obtido lá, temos:

A 1 = ∬ D 2   d x   d y = 2   ∬ D d x   d y

Passo 4

Note que ∬ D d x   d y representa o interior de um círculo de raio 1 / 2 . Portanto,

∬ D d x   d y = π 1 2 2 = π 2

Sendo assim,

A 1 = 2 π 2

Passo 5

Vamos agora calcular A 2 . Note que agora devemos parametrizar a esfera. Uma boa parametrização é a seguinte:

φ x , y = x ,   y ,   1 - x 2 - y 2

As derivadas parciais são:

∂ φ ∂ x = 1 ,   0 ,   - x 1 - x 2 - y 2 ∂ φ ∂ y = 0 ,   1 ,   - y 1 - x 2 - y 2

De modo que,

∂ φ ∂ x × ∂ φ ∂ y = i j k 1 0 - x 1 - x 2 - y 2 0 1 - y 1 - x 2 - y 2 ∂ φ ∂ x × ∂ φ ∂ y = x 1 - x 2 - y 2 , y 1 - x 2 - y 2 , 1 ∂ φ ∂ x × ∂ φ ∂ y = x 2 1 - x 2 - y 2 + y 2 1 - x 2 - y 2 + 1 ∂ φ ∂ x × ∂ φ ∂ y = x 2 + y 2 + 1 - x 2 - y 2 1 - x 2 - y 2 = 1 1 - x 2 - y 2

Passo 6

Assim, segue que

A 2 = ∬ D ∂ φ ∂ x × ∂ φ ∂ y   d x   d y = ∬ D 1 1 - x 2 - y 2 d x   d y

onde D é o interior do círculo x 2 + y 2 = 1 / 2 . Note que é uma boa fazer a mudança para coordenadas polares. Sendo assim, x = r cos ⁡ θ e y = r sin ⁡ θ , de modo que x 2 + y 2 = r 2 . Logo, e lembrando que d x   d y = r   d r   d θ ,

A 2 = ∬ D * r 1 - r 2 d r   d θ A 2 = ∫ 0 2 π ∫ 0 1 2 r 1 - r 2 d r   d θ A 2 = 2 π ∫ 0 1 2 r 1 - r 2 d r Para calcular a última integral, façamos 1 - r 2 = u . Logo, - 2 r   d r = d u ∴ r   d r = - d u 2 .

Quando r = 0 ⟹ u = 1 ; quando r = 1 2 ⟹ u = 1 2 . Finalmente, temos:

A 2 = 2 π ∫ 1 1 2 u - 1 / 2 - d u 2 A 2 = π ∫ 1 2 1 u - 1 / 2   d u A 2 = π u 1 / 2 1 / 2 1 / 2 1 A 2 = 2 π 1 - 1 2 A 2 = π 2 - 2

Passo 7

A área desejada será:

A = A 1 + A 2 A = 2 π 2 + π 2 - 2 A = π 2 4 - 2

Resposta

A área vale π 2 4 - 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma superfície S é representada pela equação vetorial r → u , v = cos ⁡ vi → + s e nvj → + uk → ,0 ≤ u ≤ 4 ,≤ v ≤ 2 π . Determinar a área de S
Calcular ∫ ∫ S x + y + zd S S é a face superior do cubo 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1 ,0 ≤ z ≤ 1 S é a face da frente do cubo do item a)
Calcular ∫ ∫ S x + y + zd S S é a face superior do cubo 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1 ,0 ≤ z ≤ 1 S é a face da frente do cubo do item a)
Calcular ∫ ∫ S x 2 zd S Onde S é a superfície cilíndrica x 2 + y 2 = 1; 0 ≤ z ≤ 1
Calcular ∫ ∫ S x + z d S Onde S é a superfície plana 2 x+ 2 y+z=6 , no 1º octante