Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.8 - Ex. 5

Calcule o comprimento da curva dada em coordenadas polares:

ρ = 1 θ     ,   1   ≤   θ   ≤   √ 3

Passo 1

Sabemos que a fórmula para o comprimento de curvas em coordenadas polares é:

∫ a b ρ 2 +   d ρ d θ 2 d θ

Logo:

ρ ² = 1 θ 2

d ρ d θ = - 1 θ 2

Passo 2

Substituindo na integral e substituindo os limites de integração que são dados no problema:

∫ 1 √ 3 1 θ 2 + 1 θ 4 d θ =   ∫ 1 √ 3 ( θ 2 + 1 ) θ ² d θ

Podemos utilizar a subsituição udv:

u= ( θ 2 + 1 ) → d u = θ θ 2 + 1 d θ

dv = d θ θ 2 → v =   - θ - 1

∫ 1 √ 3 ( θ 2 + 1 ) θ ² d θ = ( θ 2 + 1 ) * - θ - 1 +   ∫ 1 √ 3 1 θ * θ θ 2 + 1 d θ = ( θ 2 + 1 ) * - θ - 1 +     ∫ 1 √ 3 1 θ 2 + 1 d θ

Podemos usar a fórmula abaixo para a segunda interal e teremos:

( θ 2 + 1 )   *   - θ - 1 +   l n ( θ 2 +   1 ) + θ 1 3 = - 2 √ 3   +   3 ln ⁡ 2 + 3 √ 3 + 2 - l n ⁡ ( 2 +   1 )

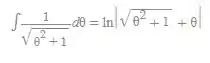
Resposta

O comprimento da curva é - 2 √ 3   +   3 ln ⁡ 2 + 3 √ 3 + 2 - l n ⁡ ( 2 +   1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quantos metros de chapa de ferro são necessários para construir um arco AB, de forma parabólica, sendo A e B simétricos com relação ao eixo de simetria da parábola e com as seguintes dimensões: 2 m a
Calcule o comprimento do gráfico da função dada.e) y = e x + e - x 2 , 0 ≤ x ≤ 1
Calcule o comprimento do gráfico da função dada.d) y = x ,1 4 ≤ x ≤ 3 4
Calcule o comprimento do gráfico da função dada.c) y = ln ⁡ x , 1 ≤ x ≤ e
Calcule o comprimento da curva dada em forma paramétrica c)x = e t cos ⁡ t y = e t sin ⁡ t0 ≤ t ≤ π