Calcule o comprimento do gráfico da função dada.

Primeiro precisamos Montar a integral que descreve o comprimento de superfície, como sabemos ela é:

Assim a primeira coisa a se fazer é achar a derivada da função, que é:

Agora substituímos:

Repara que essa integral parece complicada de resolver, mas que a raíz dela parece muito com Pitágoras.

Para esse caso vamos considerar o triângulo abaixo:

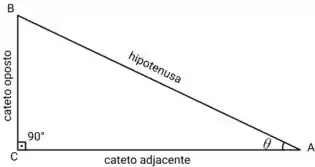
Repara que se o cateto adjacente for 2x e o cateto oposto for 1, ficamos com hipotenusa igual a . Por consequência ainda vamos ter

Esse método é chamado de Substituição trigonométrica.

Assim, substituindo teremos:

Sabemos que , então podemos usar isso para calcular essa integral com o método de integração por partes

Vimos que dv é , então assim vemos que:

Tem um lance aqui, vemos que apareceu um do lado direito, vamos jogá-lo positivo pro lado esquerdo e podemos somar os termos, ficamos com:

A integral tem um resultado tabelado que é:

Se fazemos que

Então:

Beleza! Agora só jogar os limites de integração: