Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.12 - Ex. 12
Calcule o fluxo do campo através da superfície definida pelas equações
Passo 1
Se liga! O exercício pede para calcularmos o fluxo sobre a superfície . Podemos, primeiramente, fazer um esboço dessa superfície.
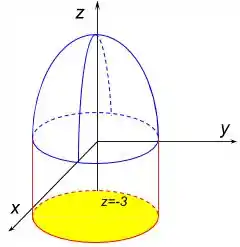
Onde a superfície em azul () é definida por
a superfície vermelha ( é definida por
e a superfície em amarelo () definida por
Passo 2
O fato da união destas superfícies formarem uma superfície fechada
Esta superfície forma um sólido que contém o ponto . Entretanto, o campo não está definido na origem. Por isso, podemos tomar uma esfera dentro no interior do sólido, centrada na origem, como mostrada na figura abaixo, cuja superfície chamaremos de , para aplicarmos o Teorema de Gauss.
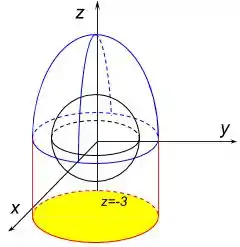
O teorema de Gauss nos fornece que
No nosso caso, temos
Onde é a região compreendida pelas superfícies e .
Passo 3
Agora podemos calcular o divergente.
Onde
Portanto
Passo 4
Substituindo na integral tripla o valor do que encontramos, temos
Repare que pela integral acima teremos 2 vezes o volume da região . Como esta região é formada por:
- Elipsoide:
- Cilindro Elíptico:
- Esfera:
O volume total será a soma dos volumes acima
Como o valor da integral nos dá 2 vezes esse valor, temos
Logo
Passo 5
Como estamos interessados no fluxo na região ,
Só precisamos calcular a integral
Para isso precisamos fazer a parametrização. Podemos usar as coordenadas esféricas
O fluxo passa a ser
E a normal
Em temos
Agora podemos reescrever nossa integral como
Podemos como essas variáveis são independentes, podemos separá-las e usando a relação , temos
Para resolver esta integral podemos a relação , portanto
Levando em consideração que nosso corresponde a , temos
Passo 6
Como vimos antes
Sendo assim