Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.12 - Ex. 6

Calcule o fluxo do campo

F x , y , z = x 3 3 + y , y 3 3 , z 3 3 + 2

através da superfície S do sólido W definido por

W = x , y , z ∈ R 3     |     x 2 + y 2 + z 2 ≥ 1 ,   x 2 + y 2 + z - 2 2 ≤ 4       e     z ≥   x 2 + y 2   ,

com campo de vetores normais a S apontando para fora.

Passo 1

Se liga! O enunciado está pedindo para encontrar o fluxo. Para começarmos a resolver, podemos escrever que o fluxo, que chamaremos de ϕ , é dado por

ϕ = ∬ S F →     .     n →   d S .

Passo 2

Podemos pegar as informações do sólido para definir a superfície de interesse

  1. x 2 + y 2 + z 2 ≥ 1 : representa uma esfera de raio ≥ 1 centrada no ponto ( 0,0 , 0 ).
  2. x 2 + y 2 + z - 2 2 ≤ 4 :   representa uma esfera de raio ≤ 2 centrada no ponto ( 0,0 , 2 )
  3. z ≥   x 2 + y 2 : representa um cone circular definido em z ≥ 0 .

Se liga no esboço da figura.

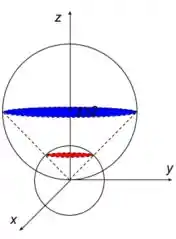
Passo 3

Agora podemos encontrar as condições para que o cone intercepte as esferas.Para a esfera ( i ):

x 2 + y 2 + z 2 = 1   ; z = x 2 + y 2

2 x 2 + 2 y 2 = 1

⇒ x 2 + y 2 = 1 2

Para a esfera ( i i ):

x 2 + y 2 + z - 2 2 = 4 ; z = x 2 + y 2

x 2 + y 2 + x 2 + y 2 - 4 x 2 + y 2 + 4 = 4

2 x 2 + 2 y 2 = 4 x 2 + y 2

x 2 + y 2 = 2 x 2 + y 2

Elevando os dois lados ao quadrado temos

x 2 + y 2 2 = 2 2 x 2 + y 2

x 2 + y 2 = 4

Passo 4

Considerando que temos uma superfície fechada, podemos aplicar o Teorema de Gauss.

∬ S F →     .   n →   d s = ∭ W d i v F → d V     ( 1 )

Onde

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z .

Fazendo as derivadas parciais, temos

∂ F 1 ∂ x = ∂ ∂ x x 3 3 = x 2

∂ F 2 ∂ y = ∂ ∂ y y 3 3 = y 2

∂ F 3 ∂ z = ∂ ∂ z z 3 3 + 2 = z 2

⇒ d i v   F → = x 2 + y 2 + z 2         ( 2 )

Portanto

∭ W d i v F → d V = ∭ D x 2 + y 2 + z 2   d z   d x   d y   ( 3 )

Passo 5

Olhando da ponta da seta do eixo z , podemos ver a figura abaixo.

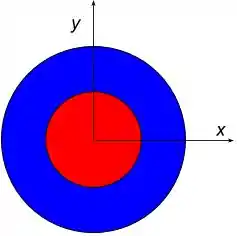
A circunferência interna tem raio 2 / 2 , região D 1 , e a externa tem raio 2 , região D 2 .

Levando em consideração a região D 1 , temos que

1 - x 2 - y 2 ≤ z ≤ 4 - x 2 - y 2 + 2

Para a região D 2 temos

x 2 + y 2 ≤ z ≤ 4 - x 2 - y 2 + 2 .

Assim podemos reescrever a integral da equação (3) como

∭ D x 2 + y 2 + z 2   d z   d x   d y = ∬ D 1 ∫ 1 - x 2 - y 2 4 - x 2 - y 2 + 2 x 2 + y 2 + z 2   d z   d x   d y + ∬ D 1 ∫ x 2 + y 2 4 - x 2 - y 2 + 2 x 2 + y 2 + z 2   d z   d x   d y         ( 4 )

Passo 6

Para facilitar nosso trabalho podemos usar mudança de coordenada. Vamos adotar as coordenadas esféricas.

x = ρ   s e n φ   c o s θ y = ρ   s e n φ   s e n θ z = ρ   c o s φ     ( 5 )

d x d y d z ⟹   ρ 2 s e n φ   d ρ   d φ   d θ

Onde

0 ≤ θ ≤ 2 π .

Como a altura e o raio do cone são iguais, podemos escrever que

0 ≤ φ ≤ π 4 .

Substituindo as relações obtidas (5) em

x 2 + y 2 + z 2 = 1

e

x 2 + y 2 + z - 2 2 = 4   ,

respectivamente, temos

ρ = 1

e

ρ = 4 c o s φ .

Passo 7

Agora podemos reescrever nossa integral

∭ D x 2 + y 2 + z 2   d z   d x   d y = ∫ 0 2 π ∫ 0 π 4   ∫ 1 4 c o s φ ρ 4   s e n φ   d ρ   d φ   d θ  

= ∫ 0 2 π ∫ 0 π 4   ρ 5 5 1 4 c o s φ   s e n φ   d ρ   d φ   d θ

= ∫ 0 2 π ∫ 0 π 4   1024 5 cos 5 ⁡ φ - 1 5   s e n φ   d ρ   d φ   d θ

= ∫ 0 2 π 1024 5 - cos 6 ⁡ φ 6 0 π 4 - 1 5 - cos ⁡ φ 0 π 4 d θ

= 1024 5 - 1 48 + 1 6 - 1 5 - 2 2 + 1 ∫ 0 2 π d θ

= 2 π 5 890 + 3 2 6 = 890 + 3 2 15 π

Passo 8

Retornando para a equação (1) temos que o fluxo será

∬ S F →     .   n →   d s = 890 + 3 2 15 π .

Resposta

∬ S F →     .   n →   d s = 890 + 3 2 15 π .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usar o teorema da divergência para calcular a integral da superfície dada. I = ∬ S 4 x - y d y d z + y 2 d z d x - x y d x d y Onde S é a superfície exterior do cubo limitado pelos planos coordenados
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = - y j ^ + z k ^ , e T o cilindro x 2 + y 2 ≤ 16 ,- 2 ≤ z ≤ 2
Verificar o teorema de Stokes para g → = 4 y i ^ - x z j ^ + y z 2 k ^ Onde S é a superfície do paraboloide 2 z = x 2 + y 2 limitado por z = 8 e C é o seu contorno percorrido no sentido anti-horário.
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S f → ⋅ n → d S Sendo f → = 2 x i ^ + 3 y j ^ + 4 z k ^ e S a superfície exterior do sólido delimitado pelos paraboloides z
Calcule o divergente do campo vetorial dado. v → x , y = - y i → + x j →