Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 3c

Calcule as integrais, para as regiões D indicadas.

(c) int int_D (x + 2 y) d x d y ; D l i m i t a d a p o r y = x^(- 2) , y = 1 e y = 4

Passo 1

E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D

Como no nosso caso temos y limitado por duas constantes, podemos considerar que a região é do tipo 2, em que ela é contínua em y e que x é limitada por funções de y . Para sabermos o intervalo de x aproveitaremos a equação de y em função de x .

Passo 2

Então, como queremos saber o intervalo de x vamos esboçar o gráfico dessa região. Temos que:

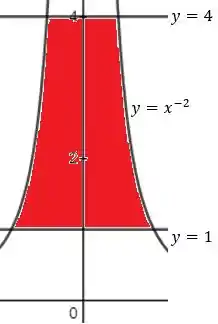
Podemos ver que os intervalos serão dados por:

1 <= y <= 4

E, para x , podemos transformar a equação da curva:

y = x^(- 2) -> y = (1)/(x^2)

Ou seja:

x^2 = (1)/(y) => x = +- (1)/(sqrt(y))

Tal que:

- (1)/(sqrt(y)) <= x <= (1)/(sqrt(y))

Passo 3

Dessa forma, podemos escrever:

int_1^4 int_(- (1)/(sqrt(y)))^((1)/(sqrt(y))) (x + 2 y) d x d y

Então, resolvendo a integral interna:

int_1^4 int_(- (1)/(sqrt(y)))^((1)/(sqrt(y))) (x + 2 y) d x d y = int_1^4 [(x^2)/(2) + 2 x y] | [[(1)/(sqrt(y))],[-,(1)/(sqrt(y))]] d y

Substituindo o intervalo de integração da integral resolvida:

=> int_1^4 [(1)/(2) ((1)/(sqrt(y)))^2 + 2 ((1)/(sqrt(y))) y - ((1)/(2) (- (1)/(sqrt(y)))^2 + 2 (- (1)/(sqrt(y))) y)] d y

O que resulta em:

=> int_1^4 [4 sqrt(y)] d y = 4 int_1^4 y^(1 // 2) d y

Passo 4

Logo, podemos resolver essa integral diretamente, tal que dessa forma:

4 int_1^4 y^(1 // 2) d y = 4 [(2)/(3) y^(3 // 2)] | [[4],[1]]

Ou seja:

=> (8)/(3) [y^(3 // 2)] | [[4],[1]]

E substituindo o intervalo de integração:

=> (8)/(3) [(4)^((3)/(2)) - (1)^((3)/(2))]

:. (8)/(3) [8 - 1] = (56)/(3)

Resposta

(56)/(3)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a transformação u = x - y ,v = x + y para avaliar ∫ ∫ R x - y x + yd A onde R é o quadrado com vértices 0 ,2 ,1 ,1 ,2 ,2 e1 ,3 .
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sr e t a sy = x ,y = x 3ey = 2
População regional: Se ƒ ( x ,y )=100( y+1ƒ ) representa a densidade populacional de uma região plana na Terra, onde x e y são medidos em milhas, encontre o número de pessoas na região delimitada pela
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. A sr e t a s y = x - 2 ey = - x
O que você acha que será maior, o valor médio de ƒ ( x ,y )=x yƒ sobre o quadrado 0≤x≤1 ,0≤y≤1 , ou o valor médio de ƒ sobre o quarto de círculo x 2+y 2≤1 no primeiro quadrante? Calcule-os para descob