Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 49

Utilize a transformação u = x - y ,   v = x + y para avaliar

∫ ∫ R x - y x + y   d A

onde R é o quadrado com vértices 0 ,   2 ,   1 ,   1 ,   2 ,   2 e   1 ,   3 .

Passo 1

Faaala pessoal, tudo na paz?! Vamos lá!

Precisamos usar a seguinte transformação:

u = x - y

v = x + y

para avaliar a integral:

∫ ∫ R x - y x + y   d A

onde R é o quadrado com vértices 0 ,   2 ,   1 ,   1 ,   2 ,   2 e   1 ,   3 .

Vamos pensar um pouco!!

Nosso primeiro objetivo é escrever x e y apenas em função de u e v . Isso a gente pode fazer considerando o sistema:

u = x - y v = x + y

Primeiro fazemos a soma para obter y   em função de u e v . Depois fazemos a subtração, ai vamos encontrar x em função de u e v .

Podemos determinar nossa região R em função de u e v , substituindo os pontos dados dos vértices do quadrado nas expressões que encontramos do sistema mencionado acima.

Antes de montar nossa integral, precisamos saber de uma coisa muito importante. Quando fazemos mudança de vari��vel, a integral vai ficar desse jeito: (obs.: deve substituir x e y pelas relações de u e v )

∫ ∫ R x - y x + y   ∂ x , y ∂ u , v d u d v

Repare que apareceu um termo em módulo que chamamos de jacobiano:

∂ x , y ∂ u , v = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

O Jacobiano é um determinante, que tem as derivadas parciais de x e y em relação a u e v .

Com todas essas informações e só montar a integral agora!!!

Vamos nessa!!!

Passo 2

Vamos começar encontrando uma relação para x e y em função de u e v .

Temos que:

u = x - y v = x + y

Somando as duas equações vamos encontrar:

2 x = u + v

x = u + v 2

Subtraindo ambas as equações temos:

- 2 y = u - v

y = v - u 2

Já encontramos as relações que queríamos:

x = u + v 2

y = v - u 2

Passo 3

Agora vamos encontrar os intervalos de u e v . Como fazemos isso?

Temos o seguinte sistema:

u = x - y v = x + y

Sabemos que nossa região R em função de   x e y é o quadrado de vértices:

0 ,   2

1 ,   1

2 ,   2

1 ,   3

Projetando esses vértices no plano x y e unindo os pontos, temos a seguinte região:

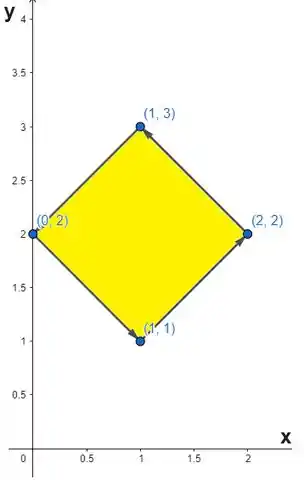
Nosso objetivo e transformar essa região, em uma região no plano u v .

Para isso, vamos substituir cada vértice nas expressões:

u = x - y v = x + y

Para o vértice 0 ,   2 , temos:

u = 0 - 2 = - 2 v = 0 + 2 = 2

Para o vértice 1 ,   1 , temos:

u = 1 - 1 = 0 v = 1 + 1 = 2

Para o vértice 2 ,   2 , temos:

u = 2 - 2 = 0 v = 2 + 2 = 4

Para o vértice 1 ,   3 , temos:

u = 1 - 3 = - 2 v = 1 + 3 = 4

Observe, que analisando os valores encontrados temos que:

- 2 ≤ u ≤ 0

2 ≤ v ≤ 4

Passo 4

Agora, estamos quase conseguindo montar a integral.

∫ ∫ R x - y x + y   ∂ x , y ∂ u , v d u d v

Já sabemos as expressões de x e y em função de ( u , v ) e os intervalos de u e v . Está faltando o Jacobiano:

∂ x , y ∂ u , v = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Vamos ter que fazer as derivadas parciais das expressões:

x = u + v 2

y = v - u 2

Lembre-se, quando derivamos em relação a u o termo v é uma constante.

Vamos fazer as derivadas. Primeiro, derivando x em relação a u e v , temos:

∂ x ∂ u = 1 2

∂ x ∂ v = 1 2

Derivando y em relação a u e v , temos:

∂ y ∂ u = - 1 2

∂ y ∂ v = 1 2

Agora é só substitui na formula do Jacobiano e determinar o determinante. Fazendo isso, vamos ter:

∂ x , y ∂ u , v = 1 / 2 1 / 2 - 1 / 2 1 / 2

Repare que temos uma matriz 2 × 2 . Assim, o determinante é igual a multiplicação da diagonal principal menos a multiplicação da diagonal secundaria.

Fazendo isso, vamos ter:

1 / 2 1 / 2 - 1 / 2 1 / 2 = 1 2 × 1 2 - - 1 2 × 1 2

Simplificando temos que:

= 1 4 + 1 4

Portanto, teremos nosso Jacobiano igual a:

∂ x , y ∂ u , v = 1 2

Passo 5

Agora sim, podemos montar nossa integral:

∫ ∫ R x - y x + y   ∂ x , y ∂ u , v d u d v

Já sabemos que x e y são:

x = u + v 2

y = v - u 2

Os intervalos são:

- 2 ≤ u ≤ 0

2 ≤ v ≤ 4

E o jacobiano é:

∂ x , y ∂ u , v = 1 2

Substituindo na integral, vamos ter:

∫ 2 4 ∫ - 2 0 u + v 2 - v - u 2 u + v 2 + v - u 2 1 2   d u   d v

Simplificando, vamos ter:

∫ 2 4 ∫ - 2 0 u 2 v   d u d v

Passo 6

Nossa ultima etapa é integrar essa expressão:

∫ 2 4 ∫ - 2 0 u 2 v   d u d v

Lembre-se, começamos integrando de dentro para fora.

Integrando em d u , vamos ter:

∫ 2 4 u 2 4 v - 2 0 d v

Aplicando os limites de integração, temos:

∫ 2 4 - 1 v d v

Integrando em d v , vamos ter:

- ln ⁡ v 2 4

Aplicando os limites de integração, temos que:

- ( ln ⁡ 4 - ln ⁡ 2 )

Podemos simplificar mais, utilizando uma das propriedades do logaritmo natural, que é:

ln ⁡ a b = ln ⁡ a - ln ⁡ b

Substituindo, temos que:

- ln ⁡ 4 2

Logo nossa resposta é:

- ln ⁡ 2

Resposta

- ln ⁡ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Como as integrais duplas são avaliadas como integrais iteradas? A ordem da integração importa? Como os limites de integração são determinados? Dê exemplos.
Como as substituições em integrais duplas são descritas comotransformações de regiões bidimensionais? Dê um exemplocom cálculo.
Carga elétrica total sobre uma placa circular A distribui-ção de carga elétrica sobre uma placa circular de raio R metrosé s(r, u) = kr(1 – sen u) coulomb/m2 (sendo k uma constante).Integre s sobre a
Água em uma antena parabólica Uma antena parabólicatem 2 m de largura e 1/2 m de profundidade. Seu eixo de simetria está inclinado 30 graus na vertical.a. Monte, mas não calcule, uma integral tripla e
Medidor parabólico de chuva Uma vasilha tem o formatodo gráfico de z = x2 + y2 de z = 0 a z = 10 pol. Você planejacalibrar a vasilha para transformá-la em um medidor de chuva. Que altura na vasilha co