Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 4ei

Calcule as integrais triplas abaixo, usando uma mudança de variáveis conveniente.

∫ ∫ ∫ W x 2 + y 2 + z 2 1 / 2 d x d y d z

Onde W é a região dada por:

i )   W = x ,   y ,   z ∈ R 3   |   x 2 + y 2 + z 2 ≤ a 2

i i )   W = x ,   y ,   z ∈ R 3   |   x 2 + y 2 + z 2 ≤ x

Passo 1

E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D

Para calcularmos a primeira integral tripla, o primeiro passo é determinar o domínio das variáveis para saber os limites de integração. No entanto, não é simplesmente determinar esses valores.

Se fizermos o esboço da superfície (mostrado a seguir) conseguimos ver que ela representa uma esfera:

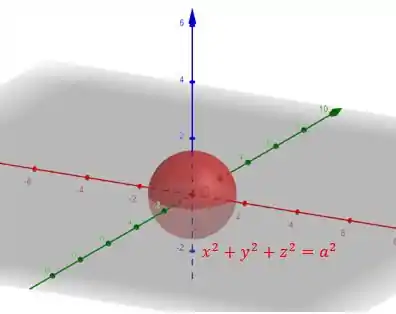
Como estaremos tratando de uma superfície esférica, no item i i ) da seção 5.10.1 (livro DIOMARA - CÁLCULO DIFERENCIAL E INTEGRAL DE FUNÇÕES DE VÁRIAS VARIÁVEIS - 1 ª ED.) temos que a substituição das variáveis x ,   y ,   z serão dadas por:

x = ρ s e n φ cos ⁡ θ

y = ρ s e n φ s e n θ

E:

z = ρ cos ⁡ φ

E a nossa integral será dada por:

∫ ∫ ∫ Q ρ s e n φ cos ⁡ θ 2 + ρ s e n φ s e n θ 2 + ρ cos ⁡ φ 2 1 / 2 ∂ x ,   y ,   z ∂ ρ ,   θ ,   φ d ρ d θ d φ

Onde:

Q = ρ ,   θ ,   φ ∈ R 3   |   ρ ≥ 0 ,     θ 0 ≤ θ ≤ θ 0 + 2 π ,     0 ≤ φ ≤ π

Seguindo o esquema das coordenadas esféricas para um ponto:

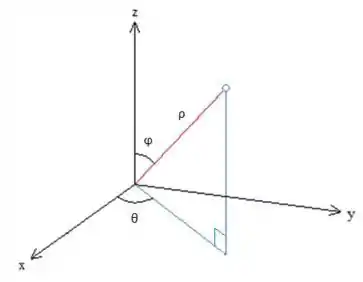
Temos que:

0 ≤ θ ≤ 2 π

E:

0 ≤ φ ≤ π

Ainda, precisamos determinar o módulo do Jacobiano. Então:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = s e n φ cos ⁡ θ - ρ s e n φ s e n θ ρ cos ⁡ φ cos ⁡ θ s e n φ s e n θ ρ s e n φ cos ⁡ θ ρ cos ⁡ φ s e n θ cos ⁡ φ 0 - ρ s e n φ

Isso resulta em:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n 3 φ cos 2 ⁡ θ - ρ 2 s e n φ cos 2 ⁡ φ s e n 2 θ

- ρ 2 s e n φ cos 2 ⁡ φ cos 2 ⁡ θ - ρ 2 s e n 3 φ s e n 2 θ

Juntando os termos semelhantes, podemos escrever:

⇒ - ρ 2 s e n 3 φ cos 2 ⁡ θ + s e n 2 θ - ρ 2 s e n φ cos 2 ⁡ φ cos 2 ⁡ θ + s e n 2 θ

Usando a identidade trigonométrica:

cos 2 ⁡ u + s e n 2 u = 1

Teremos:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n 3 φ - ρ 2 s e n φ cos 2 ⁡ φ

Ou ainda:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n φ s e n 2 φ + cos 2 ⁡ φ = - ρ 2 s e n φ

Portanto, o módulo do jacobiano é:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n φ = ρ 2 s e n φ

Dessa forma:

⇒ ∫ ∫ ∫ Q ρ 2 s e n 2 φ cos 2 ⁡ θ + ρ 2 s e n 2 φ s e n 2 θ + ρ 2 cos 2 ⁡ φ 1 / 2 ρ 2 s e n φ d ρ d θ d φ

Que fazendo o mesmo processo de juntar os termos semelhantes:

⇒ ∫ ∫ ∫ Q ρ 2 s e n 2 φ ( cos 2 ⁡ θ + s e n 2 θ )   + ρ 2 cos 2 ⁡ φ 1 / 2 ρ 2 s e n φ d ρ d θ d φ

Podemos usar a identidade trigonométrica de antes:

⇒ ∫ ∫ ∫ Q ρ 2 s e n 2 φ + ρ 2 cos 2 ⁡ φ 1 / 2 ρ 2 s e n φ d ρ d θ d φ

Fazendo isso novamente:

⇒ ∫ ∫ ∫ Q ρ 2 s e n 2 φ + cos 2 ⁡ φ 1 / 2 ρ 2 s e n φ d ρ d θ d φ

Ou ainda:

⇒ ∫ ∫ ∫ Q ρ 2 1 / 2 ρ 2 s e n φ d ρ d θ d φ = ∫ ∫ ∫ Q ρ ρ 2 s e n φ d ρ d θ d φ

Isso nos dá:

∫ ∫ ∫ W x 2 + y 2 + z 2 1 / 2 d x d y d z = ∫ ∫ ∫ Q ρ 3 s e n φ d ρ d θ d φ

Passo 2

Agora, precisamos determinar os valores que serão os intervalos de cada variável. Para isso, vamos fazer as substituições na equação da esfera. Então:

x 2 + y 2 + z 2 = a 2

Isso resulta em:

ρ 2 s e n 2 φ cos 2 ⁡ θ + ρ 2 s e n 2 φ s e n 2 θ + ρ 2 cos 2 ⁡ φ = a 2

Juntando os termos semelhantes:

ρ 2 s e n 2 φ cos 2 ⁡ θ + s e n 2 θ + ρ 2 cos 2 ⁡ φ = a 2

E lembrando (mais uma vez) da identidade trigonométrica:

cos 2 ⁡ u + s e n 2 u = 1

Podemos reescrever:

ρ 2 s e n 2 φ + ρ 2 cos 2 ⁡ φ = a 2

Tal que:

⇒ ρ 2 s e n 2 φ + cos 2 ⁡ φ = a 2

∴ ρ 2 = a 2 → ρ = ± a

Como ρ ≥ 0 , então iremos assumir:

ρ = a

Logo:

0 ≤ ρ ≤ a

Passo 3

Com todos esses resultados obtidos, podemos reescrever a integral tripla como:

∫ ∫ ∫ Q ρ 3 s e n φ d ρ d θ d φ = ∫ 0 π ∫ 0 2 π ∫ 0 a ρ 3 s e n φ d ρ d θ d φ

Ou ainda:

⇒ ∫ 0 π s e n φ ∫ 0 2 π ∫ 0 a ρ 3 d ρ d θ d φ

Então, resolvendo a primeira integral:

= ∫ 0 π s e n φ ∫ 0 2 π ρ 4 4 | a 0 d θ d φ

E substituindo o intervalo de integração:

⇒ 1 4 ∫ 0 π s e n φ ∫ 0 2 π a 4 - 0 d θ d φ

= a 4 4 ∫ 0 π s e n φ ∫ 0 2 π 1 d θ d φ

Passo 4

A segunda integral irá nos dar:

a 4 4 ∫ 0 π s e n φ ∫ 0 2 π 1 d θ d φ = a 4 4 ∫ 0 π s e n φ θ | 2 π 0 d φ

E substituindo os limites de integração:

a 4 4 ∫ 0 π s e n φ θ | 2 π 0 d φ = a 4 4 ∫ 0 π s e n φ 2 π - 0 d φ

Ou ainda:

a 4 4 ∫ 0 π s e n φ 2 π - 0 d φ = π a 4 2 ∫ 0 π s e n φ d φ

Passo 5

Por fim, a última integral resulta em:

π a 4 2 ∫ 0 π s e n φ d φ = π a 4 2 - cos ⁡ φ | π 0

E substituindo os limites de integração:

π a 4 2 - cos ⁡ φ | π 0 = π a 4 2 - cos ⁡ π - cos ⁡ 0 = π a 4 2 - - 1 - 1

∴ ∫ ∫ ∫ W x y z   d x d y d z = π a 4

Resposta

π a 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais triplas abaixo, usando uma mudança de variáveis conveniente. ∫ ∫ ∫ W d x d y d z x 2 + y 2 + z 2 Onde W é o sólido definido por: W = x ,y ,z ∈ R 3|x 2 + y 2 + z 2 ≤ 2 y ,z ≤ x 2 +
Descreva o sólido cujo volume é dado pela integral ∫ 0 π 2 ∫ 0 π 2 ∫ 1 2 ρ 2 ⋅ s e n ϕd ρd ϕd θ E calcule a integral.
Calcule o valor da integral múltipla. ∫ ∫ ∫ H z 3 ⋅x 2 + y 2 + z 2d V ondeH é o hemisfério sólido com centro na origem e raio 1 , que está acima do plano x y .
Utilize coordenadas esféricas para calcular ∫ - 2 2 ∫ 0 4 - y 2 ∫ - 4 - x 2 - y 2 4 - x 2 - y 2 y 2 ⋅ x 2 + y 2 + z 2d zd xd y
a Calcule ∫ ∫ D 1 x 2 + y 2 n 2d A , onde n é um inteiro e D é a região limitada pelos círculos com centro na origem e raios r e R , 0rR . b Para que valores de n a integral da parte a tem limite quan