Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 4d

Calcule as integrais triplas abaixo, usando uma mudança de variáveis conveniente.

∫ ∫ ∫ W x y z   d x d y d z

Onde W = x ,   y ,   z ∈ R 3   | x 2 a 2 + y 2 b 2 + z 2 c 2 ≤ 1 ,     x ≥ 0 ,     y ≥ 0 ,     z ≥ 0 .

Passo 1

E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D

Para calcularmos a integral tripla, o primeiro passo é determinar o domínio das variáveis para saber os limites de integração. No entanto, não é simplesmente determinar esses valores.

Se fizermos o esboço da superfície (mostrado a seguir) conseguimos ver que ela representa um elipsoide:

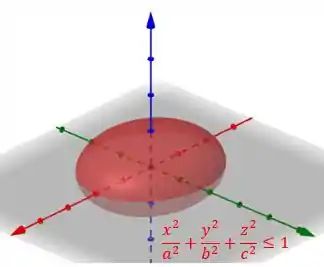
Como estaremos tratando de uma superfície esférica, no item i i ) da seção 5.10.1 (livro DIOMARA - CÁLCULO DIFERENCIAL E INTEGRAL DE FUNÇÕES DE VÁRIAS VARIÁVEIS - 1 ª ED.) temos que a substituição das variáveis x ,   y ,   z serão dadas por:

x a = ρ s e n φ cos ⁡ θ → x = a ρ s e n φ cos ⁡ θ

y b = ρ s e n φ s e n θ → y = b ρ s e n φ s e n θ

E:

z c = ρ cos ⁡ φ → z = c ρ cos ⁡ φ

E a nossa integral será dada por:

∫ ∫ ∫ W x y z   d x d y d z = ∫ ∫ ∫ Q a ρ s e n φ cos ⁡ θ b ρ s e n φ s e n θ c ρ cos ⁡ φ ∂ x ,   y ,   z ∂ ρ ,   θ ,   φ d ρ d θ d φ

Onde:

Q = ρ ,   θ ,   φ ∈ R 3   |   ρ ≥ 0 ,     θ 0 ≤ θ ≤ θ 0 + 2 π ,     0 ≤ φ ≤ π

Seguindo o esquema das coordenadas esféricas para um ponto:

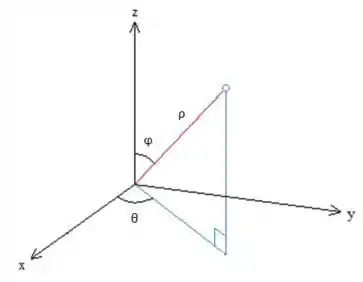
Como a região que desejamos é apenas o primeiro octante ( x ≥ 0 ,   y ≥ 0 ,   z ≥ 0 ), no nosso caso podemos ver que θ percorre apenas 1 / 4 de uma circunferência ao redor do eixo z (entre projeção do ponto no plano x y e o eixo x ) e que a região é a imagem de φ = π / 2 . Logo:

0 ≤ θ ≤ π 2

E:

0 ≤ φ ≤ π 2

Ainda, precisamos determinar o módulo do Jacobiano. Então, temos que:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = a s e n φ cos ⁡ θ - a ρ s e n φ s e n θ a ρ cos ⁡ φ cos ⁡ θ b s e n φ s e n θ b ρ s e n φ cos ⁡ θ b ρ cos ⁡ φ s e n θ c cos ⁡ φ 0 - c ρ s e n φ

Isso resulta em:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - a b c ρ 2 s e n 3 φ cos 2 ⁡ θ - a b c ρ 2 s e n φ cos 2 ⁡ φ s e n 2 θ

- a b c ρ 2 s e n φ cos 2 ⁡ φ cos 2 ⁡ θ - a b c ρ 2 s e n 3 φ s e n 2 θ

Juntando os termos semelhantes, podemos escrever:

⇒ - a b c ρ 2 s e n 3 φ cos 2 ⁡ θ + s e n 2 θ - a b c ρ 2 s e n φ cos 2 ⁡ φ cos 2 ⁡ θ + s e n 2 θ

Usando a identidade trigonométrica:

cos 2 ⁡ u + s e n 2 u = 1

Teremos:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - a b c ρ 2 s e n 3 φ - a b c ρ 2 s e n φ cos 2 ⁡ φ

Ou ainda:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - a b c ρ 2 s e n φ s e n 2 φ + cos 2 ⁡ φ = - a b c ρ 2 s e n φ

Portanto, o módulo do jacobiano é:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - a b c ρ 2 s e n φ = a b c ρ 2 s e n φ

Dessa forma:

∫ ∫ ∫ W x y z   d x d y d z = ∫ ∫ ∫ Q a b c ρ 3 cos ⁡ φ s e n 2 φ cos ⁡ θ s e n θ a b c ρ 2 s e n φ d ρ d θ d φ

Passo 2

Agora, precisamos determinar os valores que serão os intervalos de cada variável. Para isso, vamos fazer as substituições na equação do elipsoide. Então:

x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 → x a 2 + y b 2 + z c 2 = 1

Isso resulta em:

ρ 2 s e n 2 φ cos 2 ⁡ θ + ρ 2 s e n 2 φ s e n 2 θ + ρ 2 cos 2 ⁡ φ = 1

Juntando os termos semelhantes:

ρ 2 s e n 2 φ cos 2 ⁡ θ + s e n 2 θ + ρ 2 cos 2 ⁡ φ = 1

E lembrando da identidade trigonométrica:

cos 2 ⁡ u + s e n 2 u = 1

Podemos reescrever:

ρ 2 s e n 2 φ + ρ 2 cos 2 ⁡ φ = 1

Tal que:

⇒ ρ 2 s e n 2 φ cos 2 ⁡ φ = 1

∴ ρ 2 = 1 → ρ = ± 1

Como ρ ≥ 0 , então iremos assumir:

ρ = 1

Logo:

0 ≤ ρ ≤ 1

Passo 3

Com todos esses resultados obtidos, podemos reescrever a integral tripla como:

∫ ∫ ∫ Q ρ cos ⁡ φ ρ 2 s e n φ   d ρ d θ d φ = ∫ 0 π 2 ∫ 0 π 2 ∫ 0 1 a b c 2 ρ 5 cos ⁡ φ s e n 3 φ cos ⁡ θ s e n θ d ρ d θ d φ

Ou ainda:

⇒ a b c 2 ∫ 0 π 2 cos ⁡ φ s e n 3 φ ∫ 0 π 2 cos ⁡ θ s e n θ ∫ 0 1 ρ 5 d ρ d θ d φ

Então, resolvendo a primeira integral:

= a b c 2 ∫ 0 π 2 cos ⁡ φ s e n 3 φ ∫ 0 π 2 cos ⁡ θ s e n θ ρ 6 6 | 1 0 d θ d φ

E substituindo o intervalo de integração:

⇒ a b c 2 6 ∫ 0 π 2 cos ⁡ φ s e n 3 φ ∫ 0 π 2 cos ⁡ θ s e n θ 1 - 0 d θ d φ

= a b c 2 6 ∫ 0 π 2 cos ⁡ φ s e n 3 φ ∫ 0 π 2 cos ⁡ θ s e n θ d θ d φ

Passo 4

A segunda integral pode ser calculada pelo método da substituição simples com u = s e n θ , tal que d u = cos ⁡ θ d θ . Assim:

Quando θ = π 2 → u = 1

Quando θ = 0 → u = 0

Logo:

a b c 2 6 ∫ 0 π 2 cos ⁡ φ s e n 3 φ ∫ 0 π 2 cos ⁡ θ s e n θ d θ d φ = a b c 2 6 ∫ 0 π 2 cos ⁡ φ s e n 3 φ ∫ 0 1 u d u d φ

O que resulta em:

a b c 2 6 ∫ 0 π 2 cos ⁡ φ s e n 3 φ ∫ 0 1 u d u d φ = a b c 2 6 ∫ 0 π 2 cos ⁡ φ s e n 3 φ u 2 2 | 1 0 d φ

E substituindo os limites de integração:

a b c 2 6 ∫ 0 π 2 cos ⁡ φ s e n 3 φ u 2 2 | 1 0 d φ = a b c 2 12 ∫ 0 π 2 cos ⁡ φ s e n 3 φ 1 - 0 d φ

Ou ainda:

a b c 2 12 ∫ 0 π 2 cos ⁡ φ s e n 3 φ 1 - 0 d φ = a b c 2 12 ∫ 0 π 2 cos ⁡ φ s e n 3 φ d φ

Passo 5

Por fim, a última integral pode ser calculada pela mesma substituição simples com v = s e n φ , tal que d v = c o s φ d φ . Assim:

Quando φ = π 2 → v = 1

Quando φ = 0 → u = 0

Logo:

a b c 2 12 ∫ 0 π 2 cos ⁡ φ s e n 3 φ d φ = a b c 2 12 ∫ 0 1 v 3 d v

Ou seja:

a b c 2 12 ∫ 0 1 v 3 d v = a b c 2 12 v 4 4 | 1 0

E substituindo os limites de integração:

a b c 2 12 v 4 4 | 1 0 = a b c 2 48 1 - 0

∴ ∫ ∫ ∫ W x y z   d x d y d z = a b c 2 48

Resposta

a b c 2 48

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use coordenadas esféricas.
Encontre a massa e centro de massa de um hemisfério sólido com raio a e densidade proporcional a distância de sua base.
Use coordenadas esféricas.
Use coordenadas esféricas.
Use coordenadas esféricas.