Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 14

Calcule a integral dada, colocando-a em coordenadas polares.

∬ D x   d A ,

onde D é a região delimitada do primeiro quadrante compreendida entre os círculos x 2 + y 2 = 4 e x 2 + y 2 = 2 x .

Passo 1

Devemos primeiro passar a integral para coordenadas polares lembrando que d A = r   d r   d θ e que x = r cos ⁡ θ e y = r   s e n   θ .

Plotando os dois círculos, vemos que a região de integração corresponde a região pintada:

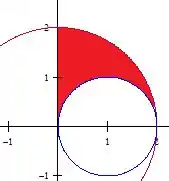
Temos que 0 ≤ θ ≤ π / 2 (primeiro quadrante) e r ≤ 2 . Por outro lado, a equação do círculo azul da

x 2 + y 2 = 2 x ⇒ r 2 = 2 r cos ⁡ θ ⇒ r = 2 cos ⁡ θ

Assim, a integral vai ser

∬ D x   d A = ∫ 0 π 2 ∫ 2 cos ⁡ θ 2 r 2 cos ⁡ θ   d r   d θ

Passo 2

Fazendo primeiro a integral em r :

∬ D x   d A = ∫ 0 π / 2 cos ⁡ θ ⋅ 8 - 8 cos 3 ⁡ θ 3     d θ = 8 3 ∫ 0 π 2 cos ⁡ θ 1 - cos 3 ⁡ θ   d θ

Assim,

∬ D x   d A = 8 3 - 8 3 ∫ 0 π 2 cos 4 ⁡ θ   d θ

Fazendo a integral,

∬ D x   d A = 8 3 - 8 3 ⋅ 3 π 16 = 8 3 - π 2

Resposta

8 3 - π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use coordenadas polares para determinar o volume do sólido dado.Abaixo do plano 2 x + y + z = 4 e acima do disco x 2 + y 2 ≤ 1 .
Use coordenadas polares para determinar o volume do sólido dado.Dentro da esfera x 2 + y 2 + z 2 = 16 e fora do cilindro x 2 + y 2 = 4 .
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 a ∫ - a 2 - y 2a 2 - y 22 x + y d x d y
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste para oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade nor
Use coordenadas polares para determinar o volume do sólido dado.Abaixo do paraboloide z = x 2 + y 2 e acima do disco x 2 + y 2 ≤ 25 .