Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.4 - Ex. 3
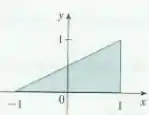
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma função qualquer contínua em .
Passo 1
A questão pede identificar que tipo de sistema de coordenadas é melhor para calcular a integral sobre a região dada e escrever a integral.
Neste caso vai ser mais simples escrever a integral em coordenas retangulares (cartesianas). Note que conforme varia no intervalo , vai do eixo () até a reta que passa pelos pontos e . A equação dessa reta é
Passo 2
Assim, escrevendo a integral temos
Resposta
Exercícios de Livros Relacionados
Use coordenadas polares para determinar o volume do sólido dado.Abaixo do plano 2 x + y + z = 4 e acima do disco x 2 + y 2 ≤ 1 .
Use coordenadas polares para determinar o volume do sólido dado.Dentro da esfera x 2 + y 2 + z 2 = 16 e fora do cilindro x 2 + y 2 = 4 .
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 a ∫ - a 2 - y 2a 2 - y 22 x + y d x d y
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste para oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade nor
Use coordenadas polares para determinar o volume do sólido dado.Abaixo do paraboloide z = x 2 + y 2 e acima do disco x 2 + y 2 ≤ 25 .