Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 22

Calcule a integral dupla.

∬ D 2 x y   d A

D é a região triangular com vértices 0 , 0 ,   ( 1 , 2 ) e ( 0 , 3 ) .

Passo 1

Primeiramente vamos analisar a região D :

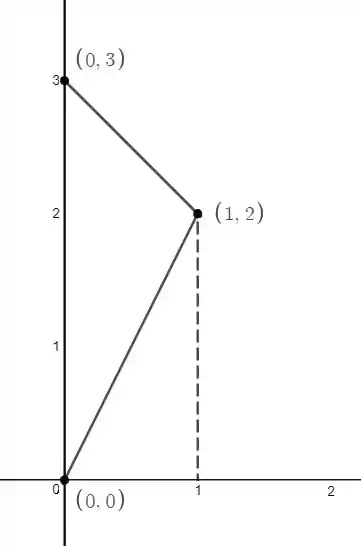
Podemos representar essa região como sendo do tipo I, com 0 ≤ x ≤ 1 e vamos analisar a variação de y

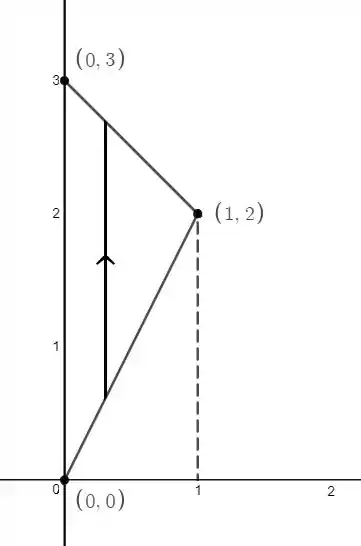
A primeira reta passa por ( 0 , 0 ) e ( 1 , 2 ) , a inclinação é

m = y 1 - y 0 x 1 - x 0 = 2 - 0 1 - 0 = 2

E a reta é

y - y 0 = m ( x - x 0 )

y - 0 = 2 ( x - 0 )

y = 2 x

A outra reta passa por ( 1 , 2 ) e ( 0 , 3 ) tem inclinação

m = 3 - 2 0 - 1 = - 1

A reta é

y - 3 = - 1 x - 0

y = - x + 3

Então podemos escrever D da seguinte forma

D = x , y   2 x ≤ y ≤ ( - x + 3 ) ,     0 ≤ x ≤ 1

Passo 2

Então temos que

∬ D 2 x y   d A = ∫ 0 1 ∫ 2 x - x + 3 2 x y   d y d x

Agora é só integrar, primeiro em relação a y

∫ 0 1 x y 2 y = 2 x y = 3 - x d x = ∫ 0 1 x 3 - x 2 - x 2 x 2 d x

= ∫ 0 1 x ( 9 - 6 x + x 2 ) - 4 x 3 d x = ∫ 0 1 9 x - 6 x 2 + x 3 - 4 x 3 d x

= ∫ 0 1 9 x - 6 x 2 - 3 x 3 d x

Agora em relação a x

= 9 x 2 2 - 2 x 3 - 3 x 4 4 0 1 = 9 2 - 2 - 3 4

= 18 - 8 - 3 4 = 7 4

Resposta

= 7 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule int_()^() int_B^() f (x , y) d x d y sendo dados:
Calcule int int_B f (x , y) d x d y sendo dados:
Calcule int int_B f (x , y) d x d y sendo dados:
Calcule int int_B f (x , y) d x d y sendo dados:
Calcule int int_B f (x , y) d x d y sendo dados: