Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 14
Calcule a integral dupla.
Passo 1
E ai turma, tudo na paz!? Partiu resolver essa!
Veja que o enunciado no forneceu uma integral dupla de uma função que é limitada pela região . A partir dessas informações e precisamos determinar o valor dessa integral.
Tá, mas e agora? Vamos com calma, beleza!?
Primeira etapa é montar a integral na ordem correta de integração. Para isso, precisamos compreender a região limitada , ou seja, vamos esboçar os gráficos das expressões
e determinar os intervalos que compreendem a região entre as duas curvas.
Importante lembrar, que sempre começamos a integrar de dentro para fora, e começamos por funções. Assim, repare uma coisa?
Ele forneceu duas funções , então sabemos que vamos variar em da função que está mais abaixo até a mais a cima. Já o intervalo em , precisamos igualar as duas funções para saber o ponto de encontro entre elas.
Logo, temos que ter uma integral com essa cara:
Você vai determinar quem é e , e a e fazendo os passos a cima.
Agora ficou fácil ein, vamos começar!?
Passo 2
Galera, pra conseguirmos escrever a integral dupla na forma iterada, primeiro precisamos descobrir quais são os limites de integração em e em .
Primeiro, vamos fazer um esboço dos gráficos das funções:
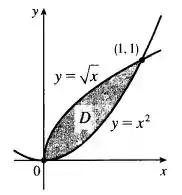
Do gráfico sabemos nossa região .
Lembra, que o intervalo de integração em vai ser da função que está mais a baixo até a função mais acima. Logo,
Assim,
Para , podemos igualar os valores de de cada curva pra achar quais são os valores de das intersecções :
Então teremos que
Assim a integral vai ficar:
Passo 3
Vamos resolver a integral. Mas lembra que a gente sempre começa resolvendo de dentro pra fora, assim:
Integrando em :
Aplicando os intervalos:
Ficamos com a integral simples em .
Passo 4
Agora, é só resolver a integral simples que restou:
Integrando em :
Aplicando os limites de integração:
Logo, a reposta da integral dupla é: