Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.2 - Ex. 20

Calcule a integral dupla.

∬ R   x x 2 + y 2   d A   ,                     R = 1 ,   2 × [ 0 ,   1 ]

Passo 1

E aiiiiii pessoal, tudo na paz!? Vamos lá!

O enunciado nos forneceu uma integral dupla, e pediu para calcularmos na região R .

∬ R   x x 2 + y 2   d A   ,                     R = 1 ,   2 × [ 0 ,   1 ]

Como vamos fazer isso?

Primeiro vamos lembrar que a região R pode ser escrita da seguinte forma:

R = 1 ,   2 × 0 ,   1 1 ≤ x ≤ 2 ,   0 ≤ y ≤ 1 }  

Assim conhecemos os limites de integração de cada variável.

Conhecemos também que d A = d x d y . Sabendo disso, podemos montar nossa integral dupla e integrar. Mas lembre-se, sempre começamos a integrar de dentro para fora.

Vamos lá iniciar os trabalhos! Partiu!!

Passo 2

Pessoal, primeiro vamos escrever a integral dupla na forma seguinte:

∫ 0 1 ∫ 1 2 x x 2 + y 2 d x   d y

Quando a gente tem uma integral dupla, a gente sempre começa resolvendo de dentro pra fora, assim:

∫ 0 1 ∫ 1 2 x x 2 + y 2 d x d y

Integrando em d x primeiro.

Calma agora. Pois precisamos aplicar uma substituição do tipo:

u = x 2 + y 2

d u d x = 2 x ∴ d u 2 = x d x

Substituindo, temos:

∫ 0 1 ∫ 1 2 1 u d u 2 d y

Vamos integrar em d u , e voltar para a variável x . Integrando:

∫ 0 1 ln ⁡ x 2 + y 2 2 1 2 d y

Aplicando os limites de integração:

∫ 0 1 1 2 ln ⁡ 4 + y 2 - ln ⁡ 1 + y 2   d y

Sabemos que a integral da soma é igual a soma da integral dos termos, logo vamos ter:

1 2 ∫ 0 1 ln ⁡ 4 + y 2   d y - ∫ 0 1 ln ⁡ 1 + y 2   d y

Passo 3

Galera, pra achar nosso resultado, ainda temos que calcular duas integrais simples em d y encontradas no passo anterior.

Pra resolver cada uma delas, teremos que usar integração por partes, do tipo:

u v - ∫ v d u

Para ficar organizado, vamos começar pela primeira integral:

∫ 0 1 ln ⁡ 4 + y 2   d y

Chamamos:

u = ln ⁡ 4 + y 2 ∴ d u = 2 y 4 + y 2 d y

d v = 1 d y ∴ v = y

Substituindo, temos:

y ln ⁡ 4 + y 2 - ∫     y   . 2 y 4 + y 2   d y

Vamos completar quadrados no numerador, para facilitar a integral. Assim:

y ln ⁡ 4 + y 2 - ∫     2 4 + y 2 - 8 4 + y 2   d y

Logo, temos:

y ln ⁡ 4 + y 2 - ∫     2 - 8 4 + y 2   d y

Lembrando que a integral da soma de termos é igual a soma das integrais. Assim:

y ln ⁡ 4 + y 2 - ∫     2   d y +   ∫     8 4 + y 2   d y

Integrando a primeira integral e dividindo tudo por 4 na segunda integral, temos que:

y ln ⁡ 4 + y 2 - 2 y + 2 ∫ 1 1 + y 2 2   d y

Essa integral, é bem conhecida né! Repare bem na integral a seguir:

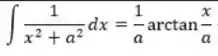
Observe que comparando, temos:

a = 1

x = y 2

Logo, nossa resposta fica:

y ln ⁡ 4 + y 2 - 2 y + 4   a r c t g y 2

Passo 4

Show! De modo bem análogo ao passo 3, faremos a outra integral:

∫ 0 1 ln ⁡ 1 + y 2   d y

Como já fizemos passo a passo na integral anterior, nessa vamos ser um pouco mais diretos.

Aplicando integrais por partes, temos que:

y ln ⁡ 1 + y 2 - ∫     y   . 2 y 1 + y 2   d y

Completando quadrados no numerador da integral:

y ln ⁡ 1 + y 2 - ∫     2 y 2 + 2 - 2 1 + y 2   d y

y ln ⁡ 1 + y 2 - ∫     2 1 + y 2 - 2 1 + y 2   d y

Agora, podemos separa os termos da integral em duas partes. Lembrando, que a integral de uma soma é igual à soma das integrais. Logo,

y ln ⁡ 1 + y 2 - ∫     2   d y + 2 ∫ 1 1 + y 2 d y

Vamos novamente, comparar a segunda integral com uma bem conhecida:

Observe que comparando, temos:

a = 1

x = y

Logo, nossa resposta fica:

y ln ⁡ 1 + y 2 - 2 y + 2   a r c t g   y

Passo 5

Agora vamos organizar o que calculamos antes.

Tínhamos a seguinte integral:

1 2 ∫ 0 1 ln ⁡ 4 + y 2   d y - ∫ 0 1 ln ⁡ 1 + y 2   d y

Obtemos cada uma separadamente, onde:

∫ 0 1 ln ⁡ 4 + y 2   d y = y ln ⁡ 4 + y 2 - 2 y + 4   a r c t g y 2

E,

∫ 0 1 ln ⁡ 1 + y 2   d y = y ln ⁡ 1 + y 2 - 2 y + 2   a r c t g   y

Bom, agora só aplicar os limites da integração nas integrais que já achamos.

1 2 y ln ⁡ 4 + y 2 - 2 y + 4   a r c t g y 2 - y ln ⁡ 1 + y 2 + 2 y - 2   a r c t g   y 0 1

Aplicando os limites, vai ficar

= 1 2 ln ⁡ 5 + 4   a r c t g 1 2 - ln ⁡ 2 - 2   a r c t g   1

Logo, nossa resposta é:

1 2 ln ⁡ 5 2 + 2   a r c t g 1 2 - π 4

Resposta

1 2 ln ⁡ 5 2 + 2   a r c t g 1 2 - π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o valor médio de f na região D . f x , y = xs e ny , D é delimitado pelas curvas y = 0 , y = x 2 e x = 1 .
No cálculo de uma integral dupla sobre uma região D , obtivemos uma soma de integrais iteradas como a que segue: ∬ D f x , yd A = ∫ 0 1 ∫ 0 2 y f x , yd xd y + ∫ 1 3 ∫ 0 3 - y f x , yd xd y Esboce a r
Use a geometria ou simetria, ou ambas, para calcular a integral dupla ∬ D 2 x + 3 y d A D é o retângulo 0 ≤ x ≤ a , 0 ≤ y ≤ b
Desenhe um exemplo de uma região que seja Tanto do tipo I quanto do tipo II;Nem do tipo I nem do tipo II.
Desenhe um exemplo de uma região que seja Do tipo I, mas não do tipo IIDo tipo II, mas não do tipo I